题目内容
14. 如图,AB是⊙O的直径,弦CD⊥AB于E,若OA=2,∠B=60°,则CD的长( )
如图,AB是⊙O的直径,弦CD⊥AB于E,若OA=2,∠B=60°,则CD的长( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 2$\sqrt{5}$ | D. | 4 |
分析 根据弦CD⊥AB于E,OA=2,∠B=60°可知CE=DE=$\frac{1}{2}$CD,设BE=x,则CE=DE=BE•tan60°=$\sqrt{3}$x,OE=2-$\sqrt{3}$x,在Rt△ODE中,根据勾股定理求出x的值,进而可得出结论.
解答 解:∵AB是⊙O的直径,弦CD⊥AB于E,OA=2,∠B=60°,
∴CE=DE=$\frac{1}{2}$CD,设BE=x,则CE=DE=BE•tan60°=$\sqrt{3}$x,OE=2-$\sqrt{3}$x,
在Rt△ODE中,OE=2-x,DE=$\sqrt{3}$x,OD=2,
∵OE2+DE2=OD2,即(2-x)2+($\sqrt{3}$x)2=22,解得x=1,
∴DE=$\sqrt{3}$,
∴CD=2DE=2$\sqrt{3}$.
故选B.
点评 本题考查的是垂径定理及勾股定理,根据题意得出OE与DE之间的关系,利用勾股定理求解是解答此题的关键.

练习册系列答案
相关题目
4.若-2am+4b4与5a2bn+1可以合并成一项,则mn的值是( )
| A. | -6 | B. | 8 | C. | -8 | D. | 9 |
19.下列四组数中,相等一组是( )
| A. | +(+3)和+(-3) | B. | +(-5)和-5 | C. | -(+4)和-(-4) | D. | +(-1)和|-1| |
3.在一个袋子里有6双运动鞋,从中任取一只运动鞋,刚好是右脚穿的运动鞋的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{12}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
 如图,已知A、B、C、D四点,根据下列要求画图:
如图,已知A、B、C、D四点,根据下列要求画图: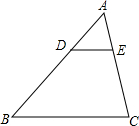 如图,在△ABC中,DE∥BC交AB于点D,交AC于点E,若DE=3,BC=9,则$\frac{AE}{AC}$=$\frac{1}{3}$.
如图,在△ABC中,DE∥BC交AB于点D,交AC于点E,若DE=3,BC=9,则$\frac{AE}{AC}$=$\frac{1}{3}$. 如图,直线MN表示一条河,A、B代表河两岸的村庄,要在河上修一座桥,使它到两个村庄的距离之和最短,问桥应建在何处?请说明理由.
如图,直线MN表示一条河,A、B代表河两岸的村庄,要在河上修一座桥,使它到两个村庄的距离之和最短,问桥应建在何处?请说明理由. 如图,在△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处.若∠A=30°,则∠ADE=30°.
如图,在△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处.若∠A=30°,则∠ADE=30°.