题目内容
4.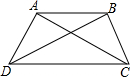 如图,AD=BC,∠ADC=∠BCD,求证:∠BAC=∠ABD.
如图,AD=BC,∠ADC=∠BCD,求证:∠BAC=∠ABD.
分析 根据全等三角形的判定与性质,可得∠ACD与∠BDC的关系,AC与BD的关系,根据等式的性质,可得∠ADB与∠BCA的关系,再根据全等三角形的判定与性质,可得答案.
解答 证明:在△ACD和△BDC中,
$\left\{\begin{array}{l}{AD=BC}\\{∠ADC=∠BCD}\\{CD=CD}\end{array}\right.$,
∴△ACD≌△BDC (SAS),
∴∠ACD=∠BDC,AC=BD.
∵∠ADC-∠BDC=∠BCD-∠ACD,
即∠ADB=∠BCA.
在△ADB和△BCA中,
$\left\{\begin{array}{l}{AD=BC}\\{∠ADB=∠BCA}\\{BD=AC}\end{array}\right.$,
∴△ADB≌△BCA (SAS),
∴∠ABD=∠BAC.
点评 本题考查了全等三角形的判定与性质,利用等式的性质得出∠ADB=∠BCA是解题关键,又利用了全等三角形的判定与性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.在一个袋子里有6双运动鞋,从中任取一只运动鞋,刚好是右脚穿的运动鞋的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{12}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
13. 如图,在△ABC中,∠ACB=90°,CD是高,∠A=30°,AB=8,则BD=( )
如图,在△ABC中,∠ACB=90°,CD是高,∠A=30°,AB=8,则BD=( )
 如图,在△ABC中,∠ACB=90°,CD是高,∠A=30°,AB=8,则BD=( )
如图,在△ABC中,∠ACB=90°,CD是高,∠A=30°,AB=8,则BD=( )| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
 如图,在△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处.若∠A=30°,则∠ADE=30°.
如图,在△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处.若∠A=30°,则∠ADE=30°. 一块模板形状如图,按规定,AB,CD的延长线的交角为85°,因交点不在模板上,不便测量,于是工人师傅连结AC,方便地测出了AB,CD的延长线相交所成的角,工人师傅是如何测量的?这块模板符合规定吗?
一块模板形状如图,按规定,AB,CD的延长线的交角为85°,因交点不在模板上,不便测量,于是工人师傅连结AC,方便地测出了AB,CD的延长线相交所成的角,工人师傅是如何测量的?这块模板符合规定吗? 如图,在⊙O中,将△OAB绕点O顺时针方向旋转80°,得到△OCD.若∠BAO=70°,则∠BOC的度数为40°.
如图,在⊙O中,将△OAB绕点O顺时针方向旋转80°,得到△OCD.若∠BAO=70°,则∠BOC的度数为40°. 实数a、b、c、m满足:$\frac{a+c}{b}$=$\frac{a+b}{c}$=$\frac{b+c}{a}$=m,那么直线y=mx-$\sqrt{2}$与如图中⊙O的位置关系为相交或相切.
实数a、b、c、m满足:$\frac{a+c}{b}$=$\frac{a+b}{c}$=$\frac{b+c}{a}$=m,那么直线y=mx-$\sqrt{2}$与如图中⊙O的位置关系为相交或相切.