题目内容
14.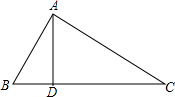 如图,在△ABC中,D是BC上一点,若AB=10,BD=6,AD=8,AC=17,求CD的长和S△ABC.
如图,在△ABC中,D是BC上一点,若AB=10,BD=6,AD=8,AC=17,求CD的长和S△ABC.
分析 在三角形ABD中,利用勾股定理的逆定理判断得到△ABD为直角三角形,即AD垂直于BC,在直角三角形ADC中,利用勾股定理求出DC的长,由BD+DC求出BC的长,即可求出三角形ABC面积.
解答 解:在△ABD中,AB=10,BD=6,AD=8,
∴AB2=BD2+AD2,
∴△ABD为直角三角形,
∴AD⊥BC,即∠ADC=90°,
在Rt△ADC中,AD=8,AC=17,
根据勾股定理得:DC=$\sqrt{A{C}^{2}-A{D}^{2}}$=15,
则S△ABC=$\frac{1}{2}$AD•BC=$\frac{1}{2}$AD•(BD+DC)=84.
点评 此题考查了勾股定理,以及三角形面积求法,熟练掌握勾股定理是解本题的关键.

练习册系列答案
相关题目
6.下列命题是真命题的是( )
| A. | 有两条边和一个角分别对应相等的两个三角形全等 | |
| B. | 两边分别相等的两个直角三角形全等 | |
| C. | 一个锐角和一条边分别相等的两个直角三角形全等 | |
| D. | 斜边和一个锐角分别相等的两个直角三角形全等 |
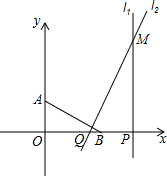 如图,点A(0,2)、B(4,0),点P从(8,0)出发,以每秒2个单位长度沿x轴向坐标原点O匀速运动,同时,点Q从B点出发,以每秒1个单位长度沿x轴向坐标原点O匀速运动,过点P作x轴的垂线l,过点Q作AB的垂线l2,它们的交点为M.设运动的时间为t(0<t<4)秒
如图,点A(0,2)、B(4,0),点P从(8,0)出发,以每秒2个单位长度沿x轴向坐标原点O匀速运动,同时,点Q从B点出发,以每秒1个单位长度沿x轴向坐标原点O匀速运动,过点P作x轴的垂线l,过点Q作AB的垂线l2,它们的交点为M.设运动的时间为t(0<t<4)秒