题目内容
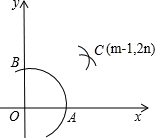
如图,在平面直角坐标系中,在x轴、y轴的正半轴上分别截取OA、OB,使OA=OB;再分别以点A、B为圆心,以大于 AB长为半径作弧,两弧交于点C.若点C的坐标为(m﹣1,2n),则m与n的关系为( )
AB长为半径作弧,两弧交于点C.若点C的坐标为(m﹣1,2n),则m与n的关系为( )
A.m+2n=1 B.m﹣2n=1 C.2n﹣m=1 D.n﹣2m=1
B
【考点】全等三角形的判定与性质;坐标与图形性质;三角形的角平分线、中线和高.
【专题】压轴题.
【分析】根据OA=OB;再分别以点A、B为圆心,以大于 AB长为半径作弧,两弧交于点C,得出C点在∠BOA的角平分线上,进而得出C点横纵坐标相等,进而得出答案.
AB长为半径作弧,两弧交于点C,得出C点在∠BOA的角平分线上,进而得出C点横纵坐标相等,进而得出答案.
【解答】解:∵OA=OB;分别以点A、B为圆心,以大于 AB长为半径作弧,两弧交于点C,
AB长为半径作弧,两弧交于点C,
∴C点在∠BOA的角平分线上,
∴C点到横纵坐标轴距离相等,进而得出,m﹣1=2n,
即m﹣2n=1.
故选:B.
【点评】此题主要考查了角平分线 的性质以及坐标点的性质,利用角平分线的作法得出C点坐标性质是解题关键.
的性质以及坐标点的性质,利用角平分线的作法得出C点坐标性质是解题关键.

练习册系列答案
相关题目

 ,3 D.2,3,4
,3 D.2,3,4 ﹣3
﹣3 +
+ .
. B.
B. C.
C. D.
D.