题目内容
9.我们把a、b、c三个数的中位数记作Z{a,b,c},直线y=kx+$\frac{1}{2}$(k>0)与函数y=Z{x,$\frac{1}{3}$x+$\frac{4}{3}$,-x}的图象有且只有2个交点,则k的取值为$\frac{1}{3}$≤k≤$\frac{3}{4}$.分析 画出函数y=Z{x2-1,x+1,-x+1}的图象,要使直线y=$\frac{1}{2}$(k>0)与函数y=Z{x,$\frac{1}{3}$x+$\frac{4}{3}$,-x}的图象有且只有2个交点,直线经过(2,2)k最大,y=kx+$\frac{1}{2}$(k>0)与AB平行时,k最小依此即可求解.
解答  解:如图,
解:如图,
图中粗线条代表Z的图象,
将A(2,2)代入,k最大,
当y=kx+$\frac{1}{2}$(k>0)与AB平行时,k最小,
∴$\frac{1}{3}$≤k≤$\frac{3}{4}$.
故答案为:$\frac{1}{3}$≤k≤$\frac{3}{4}$.
点评 本题考查了一次函数的性质以及中位数的概念,数形结合思想的应用是解题的关键.

练习册系列答案
相关题目
17.当x=1时,代数式ax3+bx+2的值是1,当x=-1时,代数式ax3+bx-2的值是( )
| A. | -2 | B. | -1 | C. | 0 | D. | 1 |
1.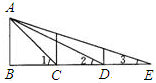 如图,∠B=90°,AB=BC=CD=DE,那么下列结论正确是( )
如图,∠B=90°,AB=BC=CD=DE,那么下列结论正确是( )
 如图,∠B=90°,AB=BC=CD=DE,那么下列结论正确是( )
如图,∠B=90°,AB=BC=CD=DE,那么下列结论正确是( )| A. | ∠1+∠2+∠3=135° | B. | △ABD∽△EBA | C. | △ACD∽△ECA | D. | 以上结论都不对 |
18.“抛一枚质地均匀的硬币,落地后正面朝上”这一事件是( )
| A. | 确定事件 | B. | 必然事件 | C. | 不可能事件 | D. | 不确定事件 |
19.下列图形中,不是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
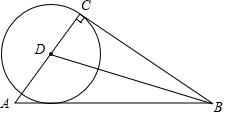 如图,Rt△ABC中,∠C=90°,BD是△ABC的平分线,交AC于点D,以点D为圆心、DC为半径作⊙D.
如图,Rt△ABC中,∠C=90°,BD是△ABC的平分线,交AC于点D,以点D为圆心、DC为半径作⊙D.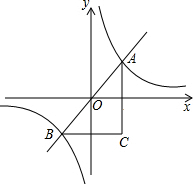 如图,反比例函数y=$\frac{2}{x}$的图象与直线y=kx(k>0)相交于A、B两点,AC∥y轴,BC∥x轴,则△ABC的面积等于4个面积单位.
如图,反比例函数y=$\frac{2}{x}$的图象与直线y=kx(k>0)相交于A、B两点,AC∥y轴,BC∥x轴,则△ABC的面积等于4个面积单位.