题目内容
17.已知$\frac{m}{n}$=$\frac{1}{2}$,则$\frac{3m-n}{m+n}$的值是$\frac{1}{3}$.分析 根据等式的性质,可用m表示n,根据分式的性质,可得答案.
解答 解:由题意,得
n=2m.
$\frac{3m-n}{m+n}$=$\frac{3m-2m}{m+2m}$=$\frac{1}{3}$,
故答案为:$\frac{1}{3}$.
点评 本题考查了比例的性质,利用等式的性质得出n=2m是解题关键.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
12.已知A(1,y1),B(-2,y2)两点在双曲线y=$\frac{m}{x}$上,且y2>y1,则m的取值范围是( )
| A. | m<0 | B. | m>0 | C. | m≥0 | D. | m≤0 |
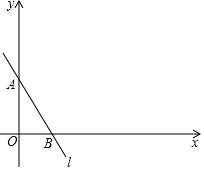 如图,已知一次函数y=-$\frac{4}{3}$x+4的图象是直线l,设直线l分别与y轴、x轴交于点A、B.
如图,已知一次函数y=-$\frac{4}{3}$x+4的图象是直线l,设直线l分别与y轴、x轴交于点A、B.