题目内容
 如图,在△ABC,∠ACB=90°,CD、CE三等分∠ACB,CD⊥AB,
如图,在△ABC,∠ACB=90°,CD、CE三等分∠ACB,CD⊥AB,求证:(1)AB=2BC;(2)CE=AE=EB.
考点:含30度角的直角三角形,直角三角形斜边上的中线
专题:证明题
分析:(1)通过已知条件可以求得∠ACE=∠ECD=∠BCD=30°,∠ECB=60°,由CD⊥AB,求得∠B=60°,则由直角三角形的两个锐角互余的性质得到∠A=30°,然后根据30°角所对的直角边等于斜边的一半,可得BC=
AB,即:AB=2BC;
(2)由(1)可知:∠A=∠ACE=30°,∠ECB=∠B=60°,然后根据等角对等边即可得:CE=AE=EB.
| 1 |
| 2 |
(2)由(1)可知:∠A=∠ACE=30°,∠ECB=∠B=60°,然后根据等角对等边即可得:CE=AE=EB.
解答:证明:(1)∵∠ACB=90°,CD,CE三等分∠ACB,
∴∠ACE=∠ECD=∠BCD=30°,∠ECB=60°,
∵CD⊥AB,
∴∠B=60°,
∴∠A=30°,
∴BC=
AB,
即:AB=2BC;
(2)由(1)可知:
∠A=∠ACE=30°,∠ECB=∠B=60°,
∴AE=CE,CE=BE,
∴AE=CE=BE.
∴∠ACE=∠ECD=∠BCD=30°,∠ECB=60°,
∵CD⊥AB,
∴∠B=60°,
∴∠A=30°,
∴BC=
| 1 |
| 2 |
即:AB=2BC;
(2)由(1)可知:
∠A=∠ACE=30°,∠ECB=∠B=60°,
∴AE=CE,CE=BE,
∴AE=CE=BE.
点评:本题考查了等腰三角形的判定和性质,等腰三角形的判定和性质,求得∠A=∠ACE,∠B=∠ECB是本题的关键.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
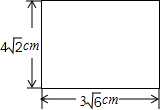 如图,已知一块矩形木板的长和宽分别为3
如图,已知一块矩形木板的长和宽分别为3| 6 |
| 2 |
现有若干个三角形,在所有的内角中,有4个直角,5个钝角,27个锐角,则在这些三角形中锐角三角形的个数是( )
| A、3 | B、4或5 | C、6或7 | D、8 |
已知方程组
的解是方程x+y=5的一个解,则m=( )
|
| A、-2 | B、-1 | C、1 | D、2 |
 如图,在平面直角坐标系中,△ABC的三个顶点A(4,3),B(1,4),C(2,1).
如图,在平面直角坐标系中,△ABC的三个顶点A(4,3),B(1,4),C(2,1).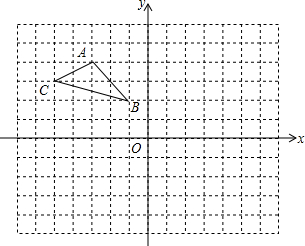 如图,在平面直角坐标系中,△ABC的三个顶点坐标为A(-3,4),B(-1,2),C(-5,3).
如图,在平面直角坐标系中,△ABC的三个顶点坐标为A(-3,4),B(-1,2),C(-5,3).
 如图,△ABC中,AB的中垂线DE交AB于E,交BC于D,若CB=10,AC=6,则△ACD的周长为
如图,△ABC中,AB的中垂线DE交AB于E,交BC于D,若CB=10,AC=6,则△ACD的周长为