题目内容
18. 二次函数y=ax2+bx+c(a≠0)的图象如图所示.
二次函数y=ax2+bx+c(a≠0)的图象如图所示.(1)求这个二次函数的解析式;
(2)根据图象,写出当x取何值时,y>0?
分析 (1)设抛物线的解析式为y=a(x+3)(x-1)(a≠0),图象过点(0,3),求出a的值,即可求出二次函数的解析式;
(2)直接根据图象写出x的取值范围.
解答 解:(1)∵图象过(-3,0),(1,0),
∴设抛物线的解析式为y=a(x+3)(x-1)(a≠0),
∵图象过(0,3),
∴3=a(0+3)(0-1),
a=-1,
∴y=-(x+3)(x-1),
即y=-x2-2x+3,
(2)由图象可知,当-3<x<1,y>0.
点评 本题主要考查了抛物线与x轴的交点以及待定系数法求二次函数的解析式,解题的关键是正确设出抛物线的解析式,此题难度不大.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
8.估计$\sqrt{20}$的大小在( )
| A. | 2与3之间 | B. | 3与4之间 | C. | 4与5之间 | D. | 5与6之间 |
13.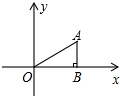 如图,在平面直角坐标系xOy中,点B在x轴的正半轴上,OB=$\sqrt{3}$,AB⊥OB,∠AOB=30°.把△ABO绕点O逆时针旋转150°后得到△A1B1O,则点A的对应点A1的坐标为( )
如图,在平面直角坐标系xOy中,点B在x轴的正半轴上,OB=$\sqrt{3}$,AB⊥OB,∠AOB=30°.把△ABO绕点O逆时针旋转150°后得到△A1B1O,则点A的对应点A1的坐标为( )
 如图,在平面直角坐标系xOy中,点B在x轴的正半轴上,OB=$\sqrt{3}$,AB⊥OB,∠AOB=30°.把△ABO绕点O逆时针旋转150°后得到△A1B1O,则点A的对应点A1的坐标为( )
如图,在平面直角坐标系xOy中,点B在x轴的正半轴上,OB=$\sqrt{3}$,AB⊥OB,∠AOB=30°.把△ABO绕点O逆时针旋转150°后得到△A1B1O,则点A的对应点A1的坐标为( )| A. | (0,-2) | B. | (-2,0) | C. | (-1,$-\sqrt{3}$) | D. | ($-\sqrt{3}$,-1) |
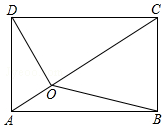 如图,已知O是矩形ABCD内一点,且OA=1,OB=3,OC=4,那么OD的长为2$\sqrt{2}$.
如图,已知O是矩形ABCD内一点,且OA=1,OB=3,OC=4,那么OD的长为2$\sqrt{2}$.