题目内容
10. 如图,在△ABC中,点E、F分别在边AC、BC上,EF∥AB,CE=$\frac{1}{2}$AE,若$\overrightarrow{AC}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,则$\overrightarrow{EF}$=$\frac{1}{3}$$\overrightarrow{a}$-$\frac{1}{3}$$\overrightarrow{b}$.
如图,在△ABC中,点E、F分别在边AC、BC上,EF∥AB,CE=$\frac{1}{2}$AE,若$\overrightarrow{AC}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,则$\overrightarrow{EF}$=$\frac{1}{3}$$\overrightarrow{a}$-$\frac{1}{3}$$\overrightarrow{b}$.
分析 由$\overrightarrow{AC}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,利用三角形法则,即可求得$\overrightarrow{AB}$,然后由EF∥AB,可证得△CEF∽△CAB,再利用相似三角形的对应边成比例,即可求得答案.
解答 解:∵$\overrightarrow{AC}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,
∴$\overrightarrow{AB}$=$\overrightarrow{AC}$-$\overrightarrow{BC}$=$\overrightarrow{a}$-$\overrightarrow{b}$,
∵EF∥AB,
∴△CEF∽△CAB,
∴$\frac{EF}{AB}=\frac{CE}{CA}$,
∵CE=$\frac{1}{2}$AE,
∴$\overrightarrow{EF}$=$\frac{1}{3}$$\overrightarrow{AB}$=$\frac{1}{3}$$\overrightarrow{a}$-$\frac{1}{3}$$\overrightarrow{b}$.
故答案为:$\frac{1}{3}$$\overrightarrow{a}$-$\frac{1}{3}$$\overrightarrow{b}$.
点评 此题考查了平面向量的知识以及相似三角形的判定与性质.注意掌握三角形法则的应用.

练习册系列答案
相关题目
5.下列事件中,是确定事件的是( )
| A. | 上海明天会下雨 | B. | 将要过马路时恰好遇到红灯 | ||
| C. | 有人把石头孵成了小鸭 | D. | 冬天,盆里的水结成了冰 |
15.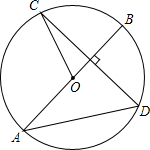 如图,线段AB是圆O的直径,弦CD⊥AB,如果∠BOC=70°,那么∠BAD等于( )
如图,线段AB是圆O的直径,弦CD⊥AB,如果∠BOC=70°,那么∠BAD等于( )
 如图,线段AB是圆O的直径,弦CD⊥AB,如果∠BOC=70°,那么∠BAD等于( )
如图,线段AB是圆O的直径,弦CD⊥AB,如果∠BOC=70°,那么∠BAD等于( )| A. | 20° | B. | 30° | C. | 35° | D. | 70° |
19.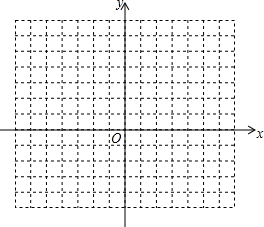 已知二次函数y=ax2+bx+c中自变量x和函数值y的部分对应值如下表:
已知二次函数y=ax2+bx+c中自变量x和函数值y的部分对应值如下表:
(1)求该二次函数的函数关系式;
(2)在所给的直角坐标系中画出此函数的图象;
(3)求出y≤10时自变量x的取值范围(可以结合图象说理).
 已知二次函数y=ax2+bx+c中自变量x和函数值y的部分对应值如下表:
已知二次函数y=ax2+bx+c中自变量x和函数值y的部分对应值如下表:| x | … | -1 | 0 | 1 | 2 | 3 | … |
| y | … | 10 | 5 | 2 | 1 | 2 | … |
(2)在所给的直角坐标系中画出此函数的图象;
(3)求出y≤10时自变量x的取值范围(可以结合图象说理).
20.下列结论正确的是( )
| A. | 对角线相等的四边形是矩形 | |
| B. | 对角线互相平分的四边形是矩形 | |
| C. | 对角线互相垂直且平分的四边形是矩形 | |
| D. | 对角线互相平分且相等的四边形是矩形 |
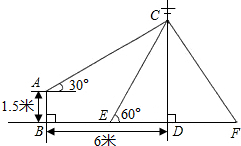 如图,在电线杆上的C处引拉线CE,CF固定电线杆,拉线CE和地面成60°角,在离电线杆6米的B是安置测角仪,在A处测得电线杆上C处的仰角为30°,已知测角仪AB的高为1.5米,求拉线CE的长($\sqrt{3}$≈1.73,结果精确到0.1米)
如图,在电线杆上的C处引拉线CE,CF固定电线杆,拉线CE和地面成60°角,在离电线杆6米的B是安置测角仪,在A处测得电线杆上C处的仰角为30°,已知测角仪AB的高为1.5米,求拉线CE的长($\sqrt{3}$≈1.73,结果精确到0.1米)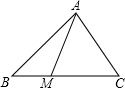 如图,在△ABC中,点M在边BC上,MC=2BM,设向量$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AM}$=$\overrightarrow{b}$,那么向量$\overrightarrow{BC}$=3$\overrightarrow{b}$-3$\overrightarrow{a}$(结果用$\overrightarrow{a}$、$\overrightarrow{b}$表示).
如图,在△ABC中,点M在边BC上,MC=2BM,设向量$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AM}$=$\overrightarrow{b}$,那么向量$\overrightarrow{BC}$=3$\overrightarrow{b}$-3$\overrightarrow{a}$(结果用$\overrightarrow{a}$、$\overrightarrow{b}$表示).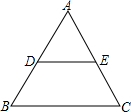 如图,等边△ABC中,点D、E分别为边AB、AC的中点,则∠DEC的度数为120°.
如图,等边△ABC中,点D、E分别为边AB、AC的中点,则∠DEC的度数为120°.