题目内容
 如图,已知在直角梯形ABCD中,AD⊥DC,AB∥DC,AB=2,DC=3,AD=7,动点P在梯形边AB、BC上,当梯形某两个顶点和动点P能构成直角三角形时,点P到AD之距离记为d,则d为________.
如图,已知在直角梯形ABCD中,AD⊥DC,AB∥DC,AB=2,DC=3,AD=7,动点P在梯形边AB、BC上,当梯形某两个顶点和动点P能构成直角三角形时,点P到AD之距离记为d,则d为________.
0≤d≤2,d= ,d=
,d= ,d=
,d= ,d=3
,d=3
分析:分①点P在AB上时,△APD是直角三角形;②点P在BC上时,△APD是直角三角形,过点P作AD的平行线与AB的延长线相交于点E,与CD相交于点F,可得四边形AEFD是矩形,根据矩形的对边相等可得EF=AD=7,AE=DF=d,然后根据△APE和△PDF相似,利用相似三角形对应边成比例可得 =
= ,再根据△PBE和△PCF相似,利用相似三角形对应边成比例可得
,再根据△PBE和△PCF相似,利用相似三角形对应边成比例可得 =
=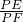 ,然后整理出只含有d的一元二次方程,求解即可;③点P在BC上时,△CDP是直角三角形,过点B作BE⊥CD于E,过点P作PF⊥AD于F,先求出CE,再利用勾股定理列式求出BC,然后利用∠C的正弦列式求出DP,再利用∠PDF的正弦列式求解即可;④点P与点C重合时,点D是直角顶点.
,然后整理出只含有d的一元二次方程,求解即可;③点P在BC上时,△CDP是直角三角形,过点B作BE⊥CD于E,过点P作PF⊥AD于F,先求出CE,再利用勾股定理列式求出BC,然后利用∠C的正弦列式求出DP,再利用∠PDF的正弦列式求解即可;④点P与点C重合时,点D是直角顶点.
解答:①点P在AB上时,△APD是直角三角形,点A是直角顶点,
∵AB=2,
∴d=AP,0<d≤2;
当点P与点A重合时,△PDC即△ADC是直角三角形,点D是直角顶点.此时d=ap=0,
综上所述,0≤d≤2.
②如图1,点P在BC上时,△APD是直角三角形,
过点P作AD的平行线与AB的延长线相交于点E,与CD相交于点F,
则四边形AEFD是矩形,
∴EF=AD=7,AE=DF=d,
∵∠APD=90°,
∴∠APE+∠DPF=90°,
∵∠PAE+∠APE=90°,
∴∠DPF=∠PAE,
又∵∠E=∠PFD=90°,
∴△APE∽△PDF,
∴ =
= ,
,
设PE=x,则PF=7-x,
∴ =
= ,
,
∴d2=-x2+7x,
∵AE∥CD,
∴ =
=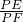 ,
,
即 =
= ,
,
∴x=7d-14,
联立 ,
,
消掉x得,50d2-245d+294=0,
解得d1= ,d2=
,d2= ;
;
③如图2,点P在BC上时,△CDP是直角三角形,
过点B作BE⊥CD于E,过点P作PF⊥AD于F,
则CE=3-2=1,BE=AD=7,
在Rt△BCE中,BC= =
= =5
=5 ,
,
sin∠C= =
= ,
,
即 =
= ,
,
解得DP= ,
,
∵∠PDF+∠PDC=90°,∠C+∠PDC=90°,
∴∠PDF=∠C,
∴d=PF=DP•sin∠PDF= ×
× =
= ;
;
④点P与点C重合时,点D是直角顶点,△ADC是直角三角形,
∴d=CD=3,
综上所述,d为0<d≤2,d= ,d=
,d= ,d=
,d= ,d=3.
,d=3.
故答案为:0<d≤2,d= ,d=
,d= ,d=
,d= ,d=3.
,d=3.
点评:本题考查了直角梯形,勾股定理的应用,相似三角形的性质,锐角三角函数,综合题,难点在于根据点P的位置分情况讨论.
 ,d=
,d= ,d=
,d= ,d=3
,d=3分析:分①点P在AB上时,△APD是直角三角形;②点P在BC上时,△APD是直角三角形,过点P作AD的平行线与AB的延长线相交于点E,与CD相交于点F,可得四边形AEFD是矩形,根据矩形的对边相等可得EF=AD=7,AE=DF=d,然后根据△APE和△PDF相似,利用相似三角形对应边成比例可得
 =
= ,再根据△PBE和△PCF相似,利用相似三角形对应边成比例可得
,再根据△PBE和△PCF相似,利用相似三角形对应边成比例可得 =
=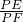 ,然后整理出只含有d的一元二次方程,求解即可;③点P在BC上时,△CDP是直角三角形,过点B作BE⊥CD于E,过点P作PF⊥AD于F,先求出CE,再利用勾股定理列式求出BC,然后利用∠C的正弦列式求出DP,再利用∠PDF的正弦列式求解即可;④点P与点C重合时,点D是直角顶点.
,然后整理出只含有d的一元二次方程,求解即可;③点P在BC上时,△CDP是直角三角形,过点B作BE⊥CD于E,过点P作PF⊥AD于F,先求出CE,再利用勾股定理列式求出BC,然后利用∠C的正弦列式求出DP,再利用∠PDF的正弦列式求解即可;④点P与点C重合时,点D是直角顶点.解答:①点P在AB上时,△APD是直角三角形,点A是直角顶点,
∵AB=2,
∴d=AP,0<d≤2;
当点P与点A重合时,△PDC即△ADC是直角三角形,点D是直角顶点.此时d=ap=0,
综上所述,0≤d≤2.
②如图1,点P在BC上时,△APD是直角三角形,
过点P作AD的平行线与AB的延长线相交于点E,与CD相交于点F,
则四边形AEFD是矩形,
∴EF=AD=7,AE=DF=d,
∵∠APD=90°,
∴∠APE+∠DPF=90°,
∵∠PAE+∠APE=90°,
∴∠DPF=∠PAE,
又∵∠E=∠PFD=90°,
∴△APE∽△PDF,
∴
 =
= ,
,
设PE=x,则PF=7-x,
∴
 =
= ,
,∴d2=-x2+7x,
∵AE∥CD,
∴
 =
=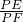 ,
,即
 =
= ,
,∴x=7d-14,
联立
 ,
,消掉x得,50d2-245d+294=0,
解得d1=
 ,d2=
,d2= ;
;③如图2,点P在BC上时,△CDP是直角三角形,
过点B作BE⊥CD于E,过点P作PF⊥AD于F,
则CE=3-2=1,BE=AD=7,
在Rt△BCE中,BC=
 =
= =5
=5 ,
,sin∠C=
 =
= ,
,即
 =
= ,
,解得DP=
 ,
,∵∠PDF+∠PDC=90°,∠C+∠PDC=90°,
∴∠PDF=∠C,
∴d=PF=DP•sin∠PDF=
 ×
× =
= ;
;④点P与点C重合时,点D是直角顶点,△ADC是直角三角形,
∴d=CD=3,
综上所述,d为0<d≤2,d=
 ,d=
,d= ,d=
,d= ,d=3.
,d=3.故答案为:0<d≤2,d=
 ,d=
,d= ,d=
,d= ,d=3.
,d=3.点评:本题考查了直角梯形,勾股定理的应用,相似三角形的性质,锐角三角函数,综合题,难点在于根据点P的位置分情况讨论.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
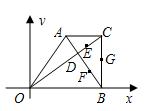 27、如图,已知在直角梯形AOBC中,AC∥OB,CB⊥OB,OB=18,BC=12,AC=9,对角线OC、AB交于点D,点E、F、G分别是CD、BD、BC的中点,以O为原点,直线OB为x轴建立平面直角坐标系,则G、E、D、F四个点中与点A在同一反比例函数图象上的是( )
27、如图,已知在直角梯形AOBC中,AC∥OB,CB⊥OB,OB=18,BC=12,AC=9,对角线OC、AB交于点D,点E、F、G分别是CD、BD、BC的中点,以O为原点,直线OB为x轴建立平面直角坐标系,则G、E、D、F四个点中与点A在同一反比例函数图象上的是( )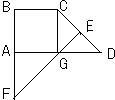 22、如图,已知在直角梯形ABCD中,BC∥AD,AB⊥AD,底AD=6,斜腰CD的垂直平分线EF交AD于G,交BA的延长线于F,且∠D=45°,求BF的长度.
22、如图,已知在直角梯形ABCD中,BC∥AD,AB⊥AD,底AD=6,斜腰CD的垂直平分线EF交AD于G,交BA的延长线于F,且∠D=45°,求BF的长度.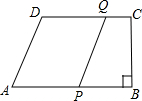 如图,已知在直角梯形ABCD中,AB∥CD,CD=9,∠B=90°,
如图,已知在直角梯形ABCD中,AB∥CD,CD=9,∠B=90°,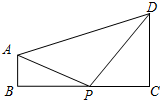 如图,已知在直角梯形ABCD中,AB∥CD,∠B=∠C=90°,AB=2,BC=7,CD=6,在BC上找一点P,使△ABP∽△DCP,求出BP的值.
如图,已知在直角梯形ABCD中,AB∥CD,∠B=∠C=90°,AB=2,BC=7,CD=6,在BC上找一点P,使△ABP∽△DCP,求出BP的值.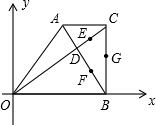 如图,已知在直角梯形AOBC中,AC∥OB,CB⊥OB,OB=18,BC=12,AC=9,对角线OC、AB交于点D,点E、F、G分别是CD、BD、BC的中点,以O为原点,直线OB为x轴建立平面直角坐标系,则G、E、D、F四个点中与点A在同一反比例函数图象上的是点
如图,已知在直角梯形AOBC中,AC∥OB,CB⊥OB,OB=18,BC=12,AC=9,对角线OC、AB交于点D,点E、F、G分别是CD、BD、BC的中点,以O为原点,直线OB为x轴建立平面直角坐标系,则G、E、D、F四个点中与点A在同一反比例函数图象上的是点