题目内容
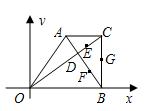 27、如图,已知在直角梯形AOBC中,AC∥OB,CB⊥OB,OB=18,BC=12,AC=9,对角线OC、AB交于点D,点E、F、G分别是CD、BD、BC的中点,以O为原点,直线OB为x轴建立平面直角坐标系,则G、E、D、F四个点中与点A在同一反比例函数图象上的是( )
27、如图,已知在直角梯形AOBC中,AC∥OB,CB⊥OB,OB=18,BC=12,AC=9,对角线OC、AB交于点D,点E、F、G分别是CD、BD、BC的中点,以O为原点,直线OB为x轴建立平面直角坐标系,则G、E、D、F四个点中与点A在同一反比例函数图象上的是( )分析:反比例函数上的点的横纵坐标的乘积相等.根据题意和图形可初步判断为点G,利用直角梯形的性质求得点A和点G的坐标即可判断.
解答:解:在直角梯形AOBC中
∵AC∥OB,CB⊥OB,OB=18,BC=12,AC=9
∴点A的坐标为(9,12)
∵点G是BC的中点
∴点G的坐标是(18,6)
∵9×12=18×6=108
∴点G与点A在同一反比例函数图象上
故选A.
∵AC∥OB,CB⊥OB,OB=18,BC=12,AC=9
∴点A的坐标为(9,12)
∵点G是BC的中点
∴点G的坐标是(18,6)
∵9×12=18×6=108
∴点G与点A在同一反比例函数图象上
故选A.
点评:此题综合考查了反比例函数与一次函数的性质,此题难度稍大,综合性比较强,注意对各个知识点的灵活应用,灵活利用直角梯形的性质求得相关点的坐标,再利用反比例函数上的点的横纵坐标的乘积相等来判断.

练习册系列答案
相关题目
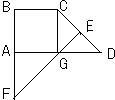 22、如图,已知在直角梯形ABCD中,BC∥AD,AB⊥AD,底AD=6,斜腰CD的垂直平分线EF交AD于G,交BA的延长线于F,且∠D=45°,求BF的长度.
22、如图,已知在直角梯形ABCD中,BC∥AD,AB⊥AD,底AD=6,斜腰CD的垂直平分线EF交AD于G,交BA的延长线于F,且∠D=45°,求BF的长度.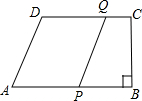 如图,已知在直角梯形ABCD中,AB∥CD,CD=9,∠B=90°,
如图,已知在直角梯形ABCD中,AB∥CD,CD=9,∠B=90°,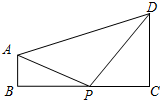 如图,已知在直角梯形ABCD中,AB∥CD,∠B=∠C=90°,AB=2,BC=7,CD=6,在BC上找一点P,使△ABP∽△DCP,求出BP的值.
如图,已知在直角梯形ABCD中,AB∥CD,∠B=∠C=90°,AB=2,BC=7,CD=6,在BC上找一点P,使△ABP∽△DCP,求出BP的值.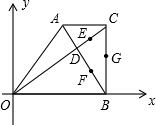 如图,已知在直角梯形AOBC中,AC∥OB,CB⊥OB,OB=18,BC=12,AC=9,对角线OC、AB交于点D,点E、F、G分别是CD、BD、BC的中点,以O为原点,直线OB为x轴建立平面直角坐标系,则G、E、D、F四个点中与点A在同一反比例函数图象上的是点
如图,已知在直角梯形AOBC中,AC∥OB,CB⊥OB,OB=18,BC=12,AC=9,对角线OC、AB交于点D,点E、F、G分别是CD、BD、BC的中点,以O为原点,直线OB为x轴建立平面直角坐标系,则G、E、D、F四个点中与点A在同一反比例函数图象上的是点