题目内容
19. 如图,数轴上顺次有A、B、D、E、P、C六个点,且任意相邻两点之间的距离都相等,点A、B、C对应的数分别为a、b、c,下列说法:①若a+b+c=0,则D为原点;②若|c|>|a|>|b|,则原点在B、D之间;③若c-b=8,则a-b=-2;④若原点在D、E之间,则|a+b|<2c,其中正确的结论有( )
如图,数轴上顺次有A、B、D、E、P、C六个点,且任意相邻两点之间的距离都相等,点A、B、C对应的数分别为a、b、c,下列说法:①若a+b+c=0,则D为原点;②若|c|>|a|>|b|,则原点在B、D之间;③若c-b=8,则a-b=-2;④若原点在D、E之间,则|a+b|<2c,其中正确的结论有( )| A. | ①②③ | B. | ①③ | C. | ③④ | D. | ①②④ |
分析 ①根据有理数加法的意义、结合数轴可得D为原点,即可求解;
②若|c|>|a|>|b|,可得原点在B、DE的中点之间,即可求解;
③若c-b=8,结合数轴可得单位长度为2,则a-b=-2,即可求解;
④若原点在D、E之间,根据有理数的加法和绝对值的性质即可求解.
解答 解:①∵数轴上顺次有A、B、D、E、P、C六个点,且任意相邻两点之间的距离都相等,a+b+c=0,
∴D为原点是正确的;
②若|c|>|a|>|b|,则原点在B、DE的中点之间,原来的说法是错误的;
③若c-b=8,
则单位长度为2,
则a-b=-2是正确的;
④若原点在D、E之间,接近E,则|a+b|>2c,原来的说法是错误的.
故选:B.
点评 此题考查了数轴和绝对值,有理数加法,用几何方法借助数轴来求解,非常直观,体现了数形结合的优点.

练习册系列答案
相关题目
4.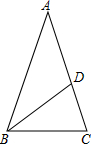 如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,则∠A等于( )
如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,则∠A等于( )
 如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,则∠A等于( )
如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,则∠A等于( )| A. | 30° | B. | 40° | C. | 36° | D. | 45° |
8.我国属于水资源缺乏的国家之一,节约用水,人人有责.某市为了强化公民的节水意思,合理利用水资源,采用价格调控手段达到节水的目的,该市自来水价格表如下:
注:水费按月结算
(1)若某户居民3月份用水4m3,则应缴水费12元;
(2)若某户居民4月份用水8m3,求应缴水费多少元?
(3)若某户居民8月份用水xm3(其中x大于5),求应缴水费多少元?(用含x的式子表示)
(4)若某户居民9月份用水18m3,则应缴水费多少元?
| 每月用水量 | 单价 |
| 不超过5m3 | 3元/m3 |
| 超过5m3不超过10m3的部分 | 5元/m3 |
| 超过10m3的部分 | 8元/m3 |
(1)若某户居民3月份用水4m3,则应缴水费12元;
(2)若某户居民4月份用水8m3,求应缴水费多少元?
(3)若某户居民8月份用水xm3(其中x大于5),求应缴水费多少元?(用含x的式子表示)
(4)若某户居民9月份用水18m3,则应缴水费多少元?
9.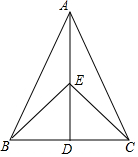 如图,在△ABC中,AB=AC,EB=EC,下列判定不正确的是( )
如图,在△ABC中,AB=AC,EB=EC,下列判定不正确的是( )
 如图,在△ABC中,AB=AC,EB=EC,下列判定不正确的是( )
如图,在△ABC中,AB=AC,EB=EC,下列判定不正确的是( )| A. | △ABD≌△ACE | B. | △ABE≌△ACE | C. | △BDE≌△CDE | D. | △ABD≌△ACD |

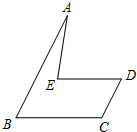 如图,已知AB∥CD,BC∥DE,若∠A=20°,∠C=120°,求∠AED的度数.
如图,已知AB∥CD,BC∥DE,若∠A=20°,∠C=120°,求∠AED的度数.