题目内容
9.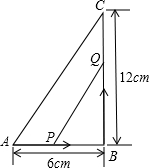 如图,在△ABC中,∠B=90°,点P从点A开始,沿AB向点B以1cm/s的速度移动,点Q从B点开始沿BC 以2cm/s的速度移动,如果P、Q分别从A、B同时出发:
如图,在△ABC中,∠B=90°,点P从点A开始,沿AB向点B以1cm/s的速度移动,点Q从B点开始沿BC 以2cm/s的速度移动,如果P、Q分别从A、B同时出发:(1)几秒后四边形APQC的面积是31平方厘米;
(2)若用S表示四边形APQC的面积,在经过多长时间S取得最小值?并求出最小值.
分析 (1)设经过x秒钟,可使得四边形APQC的面积是31平方厘米,根据面积为31列出方程,求出方程的解即可得到结果;
(2)根据题意列出S关于x的函数关系式,利用函数的性质来求最值.
解答 解:(1)设经过x秒钟,可使得四边形APQC的面积是31平方厘米,
根据题意得:$\frac{1}{2}$BP•BQ= $\frac{1}{2}$AB•BC-31,
$\frac{1}{2}$AB•BC-31,
即 $\frac{1}{2}$(6-x)•2x=$\frac{1}{2}$×6×12-31,
整理得 (x-1)(x-5)=0,
解得:x1=1,x2=5.
答:经过1或5秒钟,可使得四边形APQC的面积是31平方厘米;
(2)依题意得,S四边形APQC=S△ABC-S△BPQ,
即S=$\frac{1}{2}$AB•BC-$\frac{1}{2}$BP•BQ=$\frac{1}{2}$×6×12-$\frac{1}{2}$(6-x)•2x=(x-3)2+27(0<x<6),
当x-3=0,即x=3时,S最小=27.
答:经过3秒时,S取得最小值27平方厘米.
点评 此题考查了一元二次方程的应用、二次函数的性质,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.

练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
17.下列图形中,是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
4.下列四组数中不能构成直角三角形的一组是( )
| A. | 1,2,$\sqrt{6}$ | B. | 3,5,4 | C. | 5,12,13 | D. | 3,2,$\sqrt{13}$ |
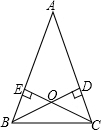 如图,在△ABC中,AB=AC,BD、CE是腰AB、AC上的高,交于点O.
如图,在△ABC中,AB=AC,BD、CE是腰AB、AC上的高,交于点O.
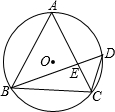 如图,已知△ABC内接于⊙O,D是⊙O上一点,连结BD、CD,AC、BD交于点E.
如图,已知△ABC内接于⊙O,D是⊙O上一点,连结BD、CD,AC、BD交于点E.