题目内容
15.在△ABC中,|sinC-$\frac{\sqrt{2}}{2}$|+($\frac{\sqrt{3}}{2}$-cosB)2=0,则∠A=( )| A. | 100° | B. | 105° | C. | 90° | D. | 60° |
分析 直接利用绝对值以及偶次方的性质得出∠C=45°,∠B=30°,进而得出答案.
解答 解:∵|sinC-$\frac{\sqrt{2}}{2}$|+($\frac{\sqrt{3}}{2}$-cosB)2=0,
∴sinC-$\frac{\sqrt{2}}{2}$=0,$\frac{\sqrt{3}}{2}$-cosB=0,
则sinC=$\frac{\sqrt{2}}{2}$,cosB=$\frac{\sqrt{3}}{2}$,
故∠C=45°,∠B=30°,
∴∠A=180°-45°-30°=105°.
故选:B.
点评 此题主要考查了特殊角的三角函数值以及偶次方的性质和绝对值的性质,正确记忆有关特殊角的三角函数值是解题关键.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
10.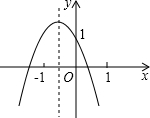 如图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面五条信息:①b2-4ac>0;②c>1;③2a-b<0;④a+b+c<0;⑤方程ax2+bx+c-1=0有两异号实数根,
如图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面五条信息:①b2-4ac>0;②c>1;③2a-b<0;④a+b+c<0;⑤方程ax2+bx+c-1=0有两异号实数根,
其中正确的有( )
 如图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面五条信息:①b2-4ac>0;②c>1;③2a-b<0;④a+b+c<0;⑤方程ax2+bx+c-1=0有两异号实数根,
如图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面五条信息:①b2-4ac>0;②c>1;③2a-b<0;④a+b+c<0;⑤方程ax2+bx+c-1=0有两异号实数根,其中正确的有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 1个 |
20.下列哪一类图形都相似?( )
| A. | 菱形 | B. | 矩形 | C. | 正方形 | D. | 梯形 |
 已知抛物线的顶点(1,1)抛物线与y轴交于点(0,2),点A为抛物线上一动点.
已知抛物线的顶点(1,1)抛物线与y轴交于点(0,2),点A为抛物线上一动点.