题目内容
10.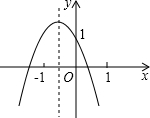 如图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面五条信息:①b2-4ac>0;②c>1;③2a-b<0;④a+b+c<0;⑤方程ax2+bx+c-1=0有两异号实数根,
如图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面五条信息:①b2-4ac>0;②c>1;③2a-b<0;④a+b+c<0;⑤方程ax2+bx+c-1=0有两异号实数根,其中正确的有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 1个 |
分析 由抛物线与x轴的交点判定b2-4ac,由抛物线与y轴的交点判断c与0的关系,根据抛物线上的对称轴与特殊点判定a+b+c,进而对所得结论进行判断.
解答 解:∵抛物线与x轴有两个交点,
∴b2-4ac>0;①正确;
∵抛物线与y轴的交点c=1,
∴②错误;
∵对称轴x=-$\frac{b}{2a}$>-1,
∴2a-b>0,③错误;
∵当x=1时,a+b+c<0,
∴④正确;
∵y=ax2+bx+c向下平移一个单位得到y=ax2+bx+c-1与x轴有两个交点,
∴程ax2+bx+c-1=0有两异号实数根,⑤正确.
正确的有①④⑤共3个.
故选:B.
点评 主要考查图象与二次函数系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换,根的判别式的熟练运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.在△ABC中,|sinC-$\frac{\sqrt{2}}{2}$|+($\frac{\sqrt{3}}{2}$-cosB)2=0,则∠A=( )
| A. | 100° | B. | 105° | C. | 90° | D. | 60° |
2.△ABC≌△DEF,且△ABC的周长为100cm,A、B分别与D、E对应,且AB=35cm,DF=30cm,则EF的长为( )
| A. | 35cm | B. | 30cm | C. | 45cm | D. | 55cm |
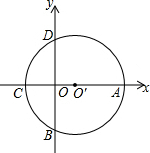 如图,在平面直角坐标系中,⊙Oˊ与两坐标轴分别交于A、B、C、D四点,已知A(6,0),C(-2,0).则点B的坐标为(0,-2$\sqrt{3}$).
如图,在平面直角坐标系中,⊙Oˊ与两坐标轴分别交于A、B、C、D四点,已知A(6,0),C(-2,0).则点B的坐标为(0,-2$\sqrt{3}$).