题目内容
6.已知等腰三角形ABC中,AB=AC,三角形的外接圆半径OB=5cm,圆心O到BC的距离为3cm,求AB的长.分析 此题分情况考虑:当三角形的外心在三角形的内部时,根据勾股定理求得BD的长,再根据勾股定理求得AB的长;当三角形的外心在三角形的外部时,根据勾股定理求得BD的长,再根据勾股定理求得AB的长.
解答 解:如图1,当三角形的外心在三角形的内部时,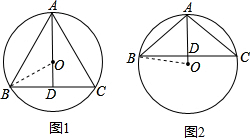
连接AO并延长到BC于点D,
∵AB=AC,O为外心,
∴AD⊥BC,
在直角三角形BOD中,根据勾股定理,得BD=4,
在直角三角形ABD中,根据勾股定理,得AB=$\sqrt{{4}^{2}+{8}^{2}}$=4$\sqrt{5}$(cm);
当三角形的外心在三角形的外部时,如图2,
在直角三角形BOD中,根据勾股定理,得BD=4,
在直角三角形ABD中,根据勾股定理,得AB=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$(cm).
即AB的长是4$\sqrt{5}$cm或2$\sqrt{5}$cm.
点评 本题考查了勾股定理的运用,能求出符合条件的所有情况时解此题的关键,注意:三角形的外心可能在三角形的外部,可能在三角形的内部,也可能在三角形的一边上,即直角三角形的外心在其斜边的中点.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
2.数轴上表示整数的点称为整点.某数轴的单位长度是1厘米,若将一根长度为24厘米的木棍放在这个数轴上,则木棍能盖住的整点的个数是( )
| A. | 22或23 | B. | 23或24 | C. | 24或25 | D. | 25或26 |
15.在△ABC中,|sinC-$\frac{\sqrt{2}}{2}$|+($\frac{\sqrt{3}}{2}$-cosB)2=0,则∠A=( )
| A. | 100° | B. | 105° | C. | 90° | D. | 60° |
16.抛物线y=x2+x+2上有点(-2,a),(-1,b),(3,c),则a,b,c的大小关系是( )
| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | 无法确定 |
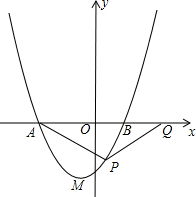 已知抛物线y=x2+2(m+1)x+4m,它与x轴分别交于原点O左侧的点A(x1,0)和右侧的点B(x2,0).
已知抛物线y=x2+2(m+1)x+4m,它与x轴分别交于原点O左侧的点A(x1,0)和右侧的点B(x2,0).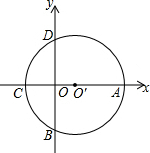 如图,在平面直角坐标系中,⊙Oˊ与两坐标轴分别交于A、B、C、D四点,已知A(6,0),C(-2,0).则点B的坐标为(0,-2$\sqrt{3}$).
如图,在平面直角坐标系中,⊙Oˊ与两坐标轴分别交于A、B、C、D四点,已知A(6,0),C(-2,0).则点B的坐标为(0,-2$\sqrt{3}$).