题目内容
5.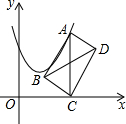 已知抛物线的顶点(1,1)抛物线与y轴交于点(0,2),点A为抛物线上一动点.
已知抛物线的顶点(1,1)抛物线与y轴交于点(0,2),点A为抛物线上一动点.(1)求此抛物线的解析式;
(2)过点A作AC⊥x轴于点C,以AC为对角线作矩形ABCD,连结BD,求对角线BD的最小值.
分析 (1)设出顶点式y=a(x-1)2+1,代入点(0,2)求得a即可;
(2)先利用配方法得到抛物线的顶点坐标为(1,1),再根据矩形的性质得BD=AC,由于AC的长等于点A的纵坐标,所以当点A在抛物线的顶点时,点A到x轴的距离最小,最小值为1,从而得到BD的最小值.
解答 解:(1)∵抛物线的顶点为(1,1),
∴抛物线的解析式y=a(x-1)2+1,代入点(0,2),
解得:a=1,
∴抛物线的解析式y=(x-1)2+1=x2-2x+2;
(2)∵抛物线的顶点坐标为(1,1),四边形ABCD为矩形,
∴BD=AC,
∵AC⊥x轴,
∴AC的长等于点A的纵坐标,
当点A在抛物线的顶点时,点A到x轴的距离最小,最小值为1,
∴对角线BD的最小值为1.
点评 本题考查了待定系数法求函数解析式,二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.也考查了矩形的性质.

练习册系列答案
相关题目
15.在△ABC中,|sinC-$\frac{\sqrt{2}}{2}$|+($\frac{\sqrt{3}}{2}$-cosB)2=0,则∠A=( )
| A. | 100° | B. | 105° | C. | 90° | D. | 60° |
16.抛物线y=x2+x+2上有点(-2,a),(-1,b),(3,c),则a,b,c的大小关系是( )
| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | 无法确定 |
17.已知|a|=3,b=5,那么a+b的值等于( )
| A. | 8 | B. | -2 | C. | 8或2 | D. | -8或-2 |
 如图,在△ABC中,AD为中线,点E在AB上,连接ED并延长,与∠DAC的平分线AF交于点F.
如图,在△ABC中,AD为中线,点E在AB上,连接ED并延长,与∠DAC的平分线AF交于点F. 如图所示,在△ABC中,AB:BC:CA=3:4:5,且周长为36cm,点P从点A开始沿AB边向B点以每秒1cm的速度移动;点Q从点B沿BC边向点C以每秒2cm的速度移动,如果同时出发,则过3秒时,△BPQ的面积为18cm2.
如图所示,在△ABC中,AB:BC:CA=3:4:5,且周长为36cm,点P从点A开始沿AB边向B点以每秒1cm的速度移动;点Q从点B沿BC边向点C以每秒2cm的速度移动,如果同时出发,则过3秒时,△BPQ的面积为18cm2.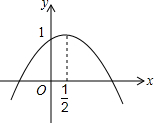 二次函数y=ax2+bx+c的图象如图所示.现有下列4个判断:①ac<0; ②a+b=0;③4ac-b2=4a;④a+b+c<0,其中正确的有( )
二次函数y=ax2+bx+c的图象如图所示.现有下列4个判断:①ac<0; ②a+b=0;③4ac-b2=4a;④a+b+c<0,其中正确的有( )