题目内容
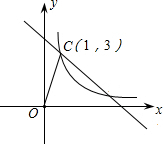 如图,反比例函数图象在第一象限的分支上有一点C(1,3),过点C的直线为y=kx+b(k<0).
如图,反比例函数图象在第一象限的分支上有一点C(1,3),过点C的直线为y=kx+b(k<0).(1)求反比例函数的解析式;
(2)如果B为反比例函数在第一象限图象上的点(点B与点C不重合),且B点的横坐标为3,在x轴上有一点P,使PC与PB的差最大,求点P的坐标.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)利用待定系数法即可求得反比例函数的解析式;
(2)首先求得B的坐标,利用待定系数法求得BC的解析式,则BC与x轴的交点就是P.
(2)首先求得B的坐标,利用待定系数法求得BC的解析式,则BC与x轴的交点就是P.
解答:解:(1)设反比例函数的解析式是y=
,
把(1,3)代入函数解析式得:k=3,
则反比例函数的解析式是y=
;
(2)在y=
中,令x=3,得y=1,则B的坐标是(3,1).
设直线BC的解析式是y=mx+n,
则
,
解得:
,
则直线BC的解析式是y=-x+4.
令y=0,解得:x=4,
则P的坐标是(4,0).
| k |
| x |
把(1,3)代入函数解析式得:k=3,
则反比例函数的解析式是y=
| 3 |
| x |
(2)在y=
| 3 |
| x |
设直线BC的解析式是y=mx+n,
则
|
解得:
|
则直线BC的解析式是y=-x+4.
令y=0,解得:x=4,
则P的坐标是(4,0).
点评:本题考查了待定系数法求函数的解析式,正确理解P的位置是关键.

练习册系列答案
相关题目
若α,β是方程x2-2x-3=0的两个实数根,则α+β的值是( )
| A、2 | B、-2 | C、3 | D、-3 |
 如图,五边形ABCDE为正五边形,以下结论正确的是( )
如图,五边形ABCDE为正五边形,以下结论正确的是( )| A、它的内角和为900° |
| B、它的外角和为540° |
| C、它共有两条对角线 |
| D、它共用五条对称轴 |
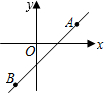 如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式1>kx+b>-2的解集为
如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式1>kx+b>-2的解集为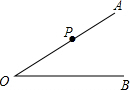 如图,已知∠AOB,P是射线OA上一点,按下列要求作图(保留作图痕迹,不要求写作法)
如图,已知∠AOB,P是射线OA上一点,按下列要求作图(保留作图痕迹,不要求写作法)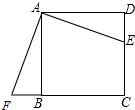 如图,在边长为6的正方形ABCD中,E是CD上一点,F在CB的延长线上,且DE=BF.
如图,在边长为6的正方形ABCD中,E是CD上一点,F在CB的延长线上,且DE=BF. 如图,已知Rt△ABC的顶点A是一次函数y=x+m与反比例函数y=
如图,已知Rt△ABC的顶点A是一次函数y=x+m与反比例函数y=