题目内容
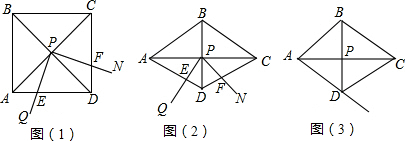
1.如图(1),∠QPN的顶点P在正方形ABCD两条对角线的交点处,∠QPN=α,将∠QPN绕点P旋转,旋转过程中∠QPN的两边分别与正方形ABCD的边AD和CD交于点E和点F(点F与点C,D不重合).(1)如图(1),当α=90°时,DE,DF,AD之间满足的数量关系是DE+DF=AD;
(2)如图(2),将图(1)中的正方形ABCD改为∠ADC=120°的菱形,其他条件不变,当α=60°时,(1)中的结论变为DE+DF=$\frac{1}{2}$AD,请给出证明;
(3)在(2)的条件下,若旋转过程中∠QPN的边PQ与AD的延长线交于点E,其他条件不变,请你探究:在运动变化过程中,(2)中的结论还成立吗?如成立,请说明理由.如不成立,请写出DE,DF,AD之间满足的数量关系,并加以证明.
分析 (1)利用正方形的性质得出角与线段的关系,易证得△APE≌△DPF,可得出AE=DF,即可得出结论DE+DF=AD,
(2)取AD的中点M,连接PM,利用菱形的性质,可得出△MDP是等边三角形,易证△MPE≌△FPD,得出ME=DF,由DE+ME=$\frac{1}{2}$AD,即可得出DE+DF=$\frac{1}{2}$AD,
(3)当点E落在AD的延长线上时,取AD的中点M,连接PM,利用菱形的性质,可得出△MDP是等边三角形,易证△MPE≌△FPD,得出ME=DF,根据线段的和差即可得到结论.
解答 解:(1)∵四边形ABCD是正方形,
∴∠APD=90°,∠PAD=PDF=45°,PA=PD,
∵∠QPN=α=90°,
∴∠APE=∠DPF=90°-∠DPE,
在△PAE和△PDF中,$\left\{\begin{array}{l}{∠PAD=∠PDF}\\{PA=PD}\\{∠APE=∠DPF}\end{array}\right.$,
∴△PAE≌△PDF,
∴DF=AE,
∴DE+DF=AD,
故答案为:DE+DF=AD;
(2)如图(1),取AD的中点M,连接PM,
∵四边形ABCD为菱形,∠ADC=120°,
∴AD=CD,∠DAP=30°,AC⊥BD,
∴∠ADP=∠CDP=60°,
∵AM=MD,
∴PM=MD,
∴△MDP是等边三角形,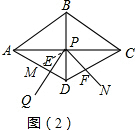
∴∠PME=∠MPD=60°,PM=PD,
∵∠QPN=60°,
∴∠MPE=∠FPD,
在△MPE和△DPF中,$\left\{\begin{array}{l}∠PME=∠PDF\\ PM=PD\\∠MPE=∠FPD\end{array}\right.$
∴△MPE≌△DPF(ASA).
∴ME=DF,
∴DE+DF=DE+ME=MD,
即DE+DF=$\frac{1}{2}$AD;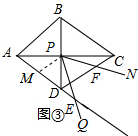
(3)如图③,当点E落在AD的延长线上时,
取AD的中点M,连接PM,
∵四边形ABCD为菱形,∠ADC=120°,
∴AD=CD,∠DAP=30°,AC⊥BD,
∴∠ADP=∠CDP=60°,
∵AM=MD,
∴PM=MD,
∴△MDP是等边三角形,
∴∠PME=∠MPD=60°,PM=PD,
∵∠QPN=60°,
∴∠MPE=∠FPD,
在△MPE和△DPF中,$\left\{\begin{array}{l}∠PME=∠PDF\\ PM=PD\\∠MPE=∠FPD\end{array}\right.$
∴△MPE≌△DPF(ASA).
∴ME=DF,
∴DF-DE=ME-DE=DM=$\frac{1}{2}$AD.
点评 本题主要考查了四边形的综合题,涉及全等三角形,正方形及菱形的性质,解答本题的关键是设计三角形全等,巧妙地借助两个三角形全等,寻找所求线段与线段之间的等量关系.

 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案 合格为了让学生更好地树立“安全第一,预防为主”的思想,河图中心学校开展了“2015秋季校园安全知识竞赛”活动,若该知识竞赛的成绩分为A(优秀),B(良好),C(合格),D(不合格)四个等级,王老师从中抽取若干名学生的成绩进行统计,并将统计结果绘制成如图所示的扇形统计图,若成绩为良好的学生比不合格的多5名,则成绩优秀的学生比合格的( )
合格为了让学生更好地树立“安全第一,预防为主”的思想,河图中心学校开展了“2015秋季校园安全知识竞赛”活动,若该知识竞赛的成绩分为A(优秀),B(良好),C(合格),D(不合格)四个等级,王老师从中抽取若干名学生的成绩进行统计,并将统计结果绘制成如图所示的扇形统计图,若成绩为良好的学生比不合格的多5名,则成绩优秀的学生比合格的( )| A. | 多5名 | B. | 少5名 | C. | 多10名 | D. | 少10名 |
| A. | x>-2 | B. | x≠0 | C. | x≥-2且x≠0 | D. | x>-2且x≠0 |
| A. | 0 | B. | $\frac{1}{3}$ | C. | -$\sqrt{9}$ | D. | π |
| A. | 55和58 | B. | 55和60 | C. | 58和58 | D. | 58和60 |
| A. | 5.464×107吨 | B. | 5.464×108吨 | C. | 5.464×109吨 | D. | 5.464×1010吨 |
 2015年我国世界环境日的主题是“践行绿色生活”.为更好地倡导市民关注环境、节约用水,政府对某小区500户家庭的用水情况进行了调查,调查小组随机抽查了其中100户家庭的月平均用水量(单位:吨),并将调查结果制成了如图所示的统计图.
2015年我国世界环境日的主题是“践行绿色生活”.为更好地倡导市民关注环境、节约用水,政府对某小区500户家庭的用水情况进行了调查,调查小组随机抽查了其中100户家庭的月平均用水量(单位:吨),并将调查结果制成了如图所示的统计图.