题目内容
6．要使$\frac{\sqrt{x+2}}{x}$有意义，则x的取值范围是（ ）| A． | x＞-2 | B． | x≠0 | C． | x≥-2且x≠0 | D． | x＞-2且x≠0 |
分析 根据二次根式有意义的条件和分式有意义的条件列出不等式，解不等式即可．
解答 解：由题意得，x+2≥0，x≠0，
解得，x≥-2且x≠0，
故选：C．
点评 本题考查的是二次根式有意义的条件和分式有意义的条件，掌握二次根式中的被开方数是非负数、分式分母不为0是解题的关键．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
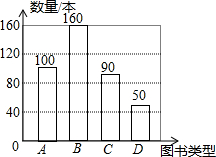王洋同学调查了光明中学图书馆中某周A，B，C，D四类图书的借阅人数（每人每次只能借阅一本图书），并绘制成了如图所示的条形统计图，若根据该条形统计图绘制扇形统计图，则B类图书借阅人数所在的扇形的圆心角的度数为144°．
16．下列根式中，是最简二次根式的是（ ）
| A． | $\sqrt{\frac{x}{3}}$ | B． | $\sqrt{8x}$ | C． | $\sqrt{6{x}^{2}}$ | D． | $\sqrt{{x}^{2}-{y}^{2}}$ |