题目内容
16.(1)解方程:$\frac{3x-2}{2}$=$\frac{4x+2}{3}$-1(2)解方程组:$\left\{\begin{array}{l}{3x-7y=8①}\\{2x+y=11②}\end{array}\right.$.
分析 (1)这是一个带分母的方程,所以要先去分母,再去括号,最后移项,合并同类项,系数化为1,从而得到方程的解;
(2)将第二个方程乘以7,然后相加,利用加减消元法求解即可.
解答 解:(1)去分母得,3(3x-2)=2(4x+2)-6,
去括号得,9x-6=8x+4-6,
移项得,9x-8x=4-6+6,
合并同类项得,x=4;
(2)$\left\{\begin{array}{l}{3x-7y=8①}\\{2x+y=11②}\end{array}\right.$,
②×7得,14x+7y=77③,
①+③得,17x=85,
解得x=5,
将x=5代入②得,2×5+y=11,
解得y=1,
所以,方程组的解是$\left\{\begin{array}{l}{x=5}\\{y=1}\end{array}\right.$.
点评 本题考查了解一元一次方程,注意在去分母时,方程两端同乘各分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子(如果是一个多项式)作为一个整体加上括号;二元一次方程组的解法,方程组中未知数的系数较小时可用代入法,当未知数的系数相等或互为相反数时用加减消元法较简单.

练习册系列答案
相关题目
11.对多项式3x2-3x因式分解,提取的公因式为( )
| A. | 3 | B. | x | C. | 3x | D. | 3x2 |
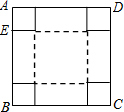 某数学兴趣小组想用一张边长为20cm的正方形纸片ABCD(如图),制作一个无盖长方体盒子,设剪去的小正方形的边长AE=xcm.
某数学兴趣小组想用一张边长为20cm的正方形纸片ABCD(如图),制作一个无盖长方体盒子,设剪去的小正方形的边长AE=xcm.