题目内容
如图，△ABM≌△CDN，则下列关系成立的是（ ）| A、∠A=∠D |
| B、AM=MB |
| C、∠M=∠N |
| D、AC=BC |
考点：全等三角形的性质
专题：
分析：根据全等三角形的性质得出∠A=∠NCD，AM=CN，∠M=∠N，∠D=∠MBA，AB=CD，求出AC=BD，即可得出选项．
解答：解：∵△ABM≌△CDN，
∴∠A=∠NCD，AM=CN，∠M=∠N，∠D=∠MBA，AB=CD，
∴AB-BC=CD-BC，
∴AC=BD，
即只有选项C正确，选项A、B、D都错误，
故选C．
∴∠A=∠NCD，AM=CN，∠M=∠N，∠D=∠MBA，AB=CD，
∴AB-BC=CD-BC，
∴AC=BD，
即只有选项C正确，选项A、B、D都错误，
故选C．
点评：本题考查了全等三角形的性质的应用，注意：全等三角形的对应边相等，对应角相等．
练习册系列答案
相关题目
如图，在锐角△ABC中，CD、BE分别是AB、AC边上的高，且CD、BE相交于点P，若∠A=50°，则∠BPC=
如图，已知AB∥DE，AF=DC，AB=DE．
如图，在△ABC中，∠ADE=∠ACD=∠ABC，则图中相似三角形有（ ）对．| A、1 | B、2 | C、3 | D、4 |
如图，已知∠A=∠F，∠C=∠D，试说明BD∥CE．下列说法不正确的是（ ）
| A、任何一个有理数的绝对值都是正数 |
| B、0既不是正数也不是负数 |
| C、有理数可以分为正有理数，负有理数和零 |
| D、0的绝对值等于0 |
已知⊙O1和⊙O2相切，⊙O1和⊙O2的半径分别是方程x2-5x+6=0的解，则O1O2的长是（ ）
| A、1 | B、5 |
| C、1或5 | D、0.5或2.5 |
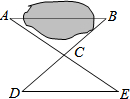如图，有一池塘，要测量池塘两端A、B的距离，可先在平地上取一个可以直接到达A和B的点C，连结AC并延长至E，使CE=AC，连结BC并延长至D，使CD=BC，连结DE，根据△ABC≌△EDC可知，量出DE的长，就是A、B的距离，这里△ABC≌△EDC的依据是（ ）