题目内容
17.利用等式性质变形正确的是( )| A. | 若ab=ac,则b=c | B. | 若a=b,则$\frac{a}{{c}^{2}+1}$=$\frac{b}{{c}^{2}+1}$ | ||
| C. | 若$\frac{b}{a}$=$\frac{c}{a}$两边都除以a,可得b=c | D. | 若S=ab,则b=$\frac{s}{a}$ |
分析 根据等式的性质即可判断.
解答 解:(A)当a=0时,此时b≠c,故A错误;
(C)若$\frac{b}{a}=\frac{c}{a}$两边同时乘以a可得b=c,故C错误;
(D)当a=0时,$\frac{S}{a}$无意义,故D错误;
故选(B)
点评 本题考查等式的性质,属于基础题型.

练习册系列答案
相关题目
7.(axay)10=a20( a>0,且 a≠0),则 x、y 的关系是( )
| A. | xy=2 | B. | x+y=10 | C. | x+y=2 | D. | x=$\frac{y}{10}$ |
5.点A、B在直线l的同侧,AB=3cm,点C是点B关于直线l的对称点,AC交直线l于点D,AC=5cm,则△ABD的周长为( )
| A. | 5cm | B. | 6cm | C. | 8cm | D. | 9cm |
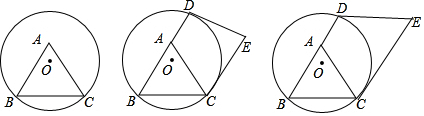
 如图,点A、C和B都在⊙O上,且AC∥OB,BC∥OA
如图,点A、C和B都在⊙O上,且AC∥OB,BC∥OA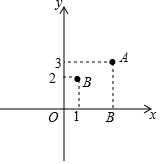 在平面直角坐标系中,点A的坐标为(3,3),点B的坐标为(1,2).
在平面直角坐标系中,点A的坐标为(3,3),点B的坐标为(1,2).