题目内容
已知多项式3x2+my-8与多项式-nx2+2y+7的和中,不含有x、y,求m(m+n).
考点:整式的加减
专题:
分析:先求出两个多项式的和,再根据题意,不含有x、y,即含x、y项的系数为0,求得m,n的值,再代入m(m+n)求值即可.
解答:解:(3x2+my-8)+(-nx2+2y+7)
=3x2+my-8-nx2+2y+7
=(3-n)x2+(m+2)y-1,
因为不含有x、y,所以3-n=0,m+2=0,
解得n=3,m=-2,
把n=-3,m=2代入m(m+n)=-2(-2+3)=-2.
=3x2+my-8-nx2+2y+7
=(3-n)x2+(m+2)y-1,
因为不含有x、y,所以3-n=0,m+2=0,
解得n=3,m=-2,
把n=-3,m=2代入m(m+n)=-2(-2+3)=-2.
点评:本题考查了整式的加减,当一个多项式中不含有哪一项时,应让那一项的系数为0.整式的加减运算实际上就是去括号、合并同类项,这是各地中考的常考点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
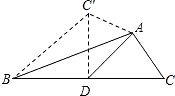 如图,AD是△ABC的中线,∠ADC=45°,把△ADC沿AD对折,使点C落在点C′的位置,则图中的一个等腰直角三角形是( )
如图,AD是△ABC的中线,∠ADC=45°,把△ADC沿AD对折,使点C落在点C′的位置,则图中的一个等腰直角三角形是( )| A、△ADC | B、△BDC′ |
| C、△ADC′ | D、不存在 |
 如图,抛物线y=x2+2x+b与x轴交于点B,且A点坐标为(3,0),B点坐标为(0,3).
如图,抛物线y=x2+2x+b与x轴交于点B,且A点坐标为(3,0),B点坐标为(0,3). 从正面、左面、上面观察如图所示的几何体,分别画出你所看到的几何体的形状图.
从正面、左面、上面观察如图所示的几何体,分别画出你所看到的几何体的形状图.