题目内容
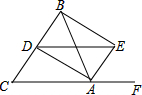 如图,△ABC中,AB=AC,F是CA延长线上一点,AD、AE分别平分∠BAC和∠BAF,BE⊥AE,说明:AB=DE.
如图,△ABC中,AB=AC,F是CA延长线上一点,AD、AE分别平分∠BAC和∠BAF,BE⊥AE,说明:AB=DE.考点:等腰三角形的判定与性质
专题:证明题
分析:根据等腰三角形三线合一的性质得出∠ADB=90°,因为∠BAC和∠BAF是邻补角,即可得出∠DAE=90°,然后根据BE⊥AE,即可判定四边形BDAE是矩形,根据矩形的性质即可证得结论.
解答:证明:∵AB=AC,AD平分∠BAC,
∴AD⊥BC,
∴∠ADB=90°
∵AD、AE分别平分∠BAC和∠BAF,
∴∠DAE=90°,
∵BE⊥AE,
∴∠AEB=90°,
∴四边形BDAE是矩形,
∴AB=DE.
∴AD⊥BC,
∴∠ADB=90°
∵AD、AE分别平分∠BAC和∠BAF,
∴∠DAE=90°,
∵BE⊥AE,
∴∠AEB=90°,
∴四边形BDAE是矩形,
∴AB=DE.
点评:本题考查了等腰三角形的性质,矩形的判定和性质,熟练掌握性质定理是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
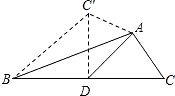 如图,AD是△ABC的中线,∠ADC=45°,把△ADC沿AD对折,使点C落在点C′的位置,则图中的一个等腰直角三角形是( )
如图,AD是△ABC的中线,∠ADC=45°,把△ADC沿AD对折,使点C落在点C′的位置,则图中的一个等腰直角三角形是( )| A、△ADC | B、△BDC′ |
| C、△ADC′ | D、不存在 |
 从正面、左面、上面观察如图所示的几何体,分别画出你所看到的几何体的形状图.
从正面、左面、上面观察如图所示的几何体,分别画出你所看到的几何体的形状图. 如图,△ABC绕点C旋转后,顶点A的对应点为点D,若∠A=70°,∠B=80°,∠ACE=65°,则旋转角度的度数为
如图,△ABC绕点C旋转后,顶点A的对应点为点D,若∠A=70°,∠B=80°,∠ACE=65°,则旋转角度的度数为 如图,△ABC为等边三角形,D是BC边上的一点,△ABD经过旋转后到达△ACE的位置.
如图,△ABC为等边三角形,D是BC边上的一点,△ABD经过旋转后到达△ACE的位置. 分别在下图中画出△ABC绕点O顺时针旋转90°和180°后的图形.
分别在下图中画出△ABC绕点O顺时针旋转90°和180°后的图形.