题目内容
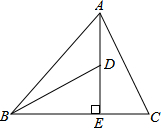 已知在△ABC中,AE⊥BC于E,AE=BE,D是AE上一点,且DE=CE,连接BD,AC,试判断BD与AC的位置关系与数量关系,并说明理由.
已知在△ABC中,AE⊥BC于E,AE=BE,D是AE上一点,且DE=CE,连接BD,AC,试判断BD与AC的位置关系与数量关系,并说明理由.考点:全等三角形的判定与性质
专题:
分析:AC与BD的关系为:AC=BD;AC⊥BD.根据SAS即可证明△AEC≌△BED,根据全等三角形的对应边相等,即可证得;根据△AEC≌△BED可以得到:∠CAE=∠EBD,根据三角形内角和定理可得:∠BFC=90°,即可证明垂直关系.
解答:解:AC与DE的关系为:①AC=BD;②AC⊥BD,
理由如下: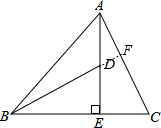
①∵AE⊥CB
∴∠AEC=∠BED=90°.
在△AEC和△BED中
∴△AEC≌△BED,
∴AC=BD,
②∵△AEC≌△BED,
∴∠CAE=∠EBD,
∵∠AEC=90°,
∴∠C+∠CAE=90°,
∴∠CBF+∠C=90°,
∴∠BFC=90°,
∴AC⊥BD.
理由如下:

①∵AE⊥CB
∴∠AEC=∠BED=90°.
在△AEC和△BED中
|
∴△AEC≌△BED,
∴AC=BD,
②∵△AEC≌△BED,
∴∠CAE=∠EBD,
∵∠AEC=90°,
∴∠C+∠CAE=90°,
∴∠CBF+∠C=90°,
∴∠BFC=90°,
∴AC⊥BD.
点评:本题考查了三角形全等的判定与性质,以及垂直关系的证明,证明三角形全等是解此题的关键.

练习册系列答案
相关题目
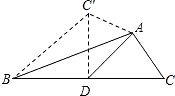 如图,AD是△ABC的中线,∠ADC=45°,把△ADC沿AD对折,使点C落在点C′的位置,则图中的一个等腰直角三角形是( )
如图,AD是△ABC的中线,∠ADC=45°,把△ADC沿AD对折,使点C落在点C′的位置,则图中的一个等腰直角三角形是( )| A、△ADC | B、△BDC′ |
| C、△ADC′ | D、不存在 |
 如图,△ABC绕点C旋转后,顶点A的对应点为点D,若∠A=70°,∠B=80°,∠ACE=65°,则旋转角度的度数为
如图,△ABC绕点C旋转后,顶点A的对应点为点D,若∠A=70°,∠B=80°,∠ACE=65°,则旋转角度的度数为 已知如图,AD平分∠BAC,∠BAC+∠ACD=180°,点E在AD上,BE的延长线交CD于F,连CE,且AB=AC.求证:∠1=∠2.
已知如图,AD平分∠BAC,∠BAC+∠ACD=180°,点E在AD上,BE的延长线交CD于F,连CE,且AB=AC.求证:∠1=∠2.