题目内容
11. 如图,在△ABD和△CDB中,AD=CB,AB、CD相交于点O,请你补充一个条件,使得△AOD≌△COB.你补充的条件是∠A=∠C.
如图,在△ABD和△CDB中,AD=CB,AB、CD相交于点O,请你补充一个条件,使得△AOD≌△COB.你补充的条件是∠A=∠C.
分析 此题是一道开放型的题目,答案不唯一,如还可以∠ADO=∠CBO.
解答 解:∠A=∠C,
理由是:∵在△AOD和△COB中
$\left\{\begin{array}{l}{∠AOD=∠COB}\\{∠A=∠C}\\{AD=BC}\end{array}\right.$
∴△AOD≌△COB(AAS),
故答案为:∠A=∠C.
点评 本题考查了全等三角形的判定定理的应用,能正确应用全等三角形的判定定理进行推理是解此题的关键,难度适中.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
19.你对“0”有多少了解?下列关于“0”的说法错误的是( )
| A. | 任何数与0相乘都得0 | B. | 0是最小的有理数 | ||
| C. | 绝对值最小的有理数是0 | D. | 0没有倒数 |
6.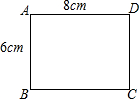 在一张长为8cm,宽为6cm的矩形纸片上,要剪下一个腰长为5cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的顶点A重合,其余的两个顶点都在矩形的边上).这个等腰三角形有几种剪法?( )
在一张长为8cm,宽为6cm的矩形纸片上,要剪下一个腰长为5cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的顶点A重合,其余的两个顶点都在矩形的边上).这个等腰三角形有几种剪法?( )
 在一张长为8cm,宽为6cm的矩形纸片上,要剪下一个腰长为5cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的顶点A重合,其余的两个顶点都在矩形的边上).这个等腰三角形有几种剪法?( )
在一张长为8cm,宽为6cm的矩形纸片上,要剪下一个腰长为5cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的顶点A重合,其余的两个顶点都在矩形的边上).这个等腰三角形有几种剪法?( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
3.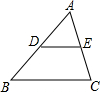 如图,DE是△ABC的一条中位线,若△ADE的面积为2,则四边形DBCE的面积为( )
如图,DE是△ABC的一条中位线,若△ADE的面积为2,则四边形DBCE的面积为( )
 如图,DE是△ABC的一条中位线,若△ADE的面积为2,则四边形DBCE的面积为( )
如图,DE是△ABC的一条中位线,若△ADE的面积为2,则四边形DBCE的面积为( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
20.a为任意实数时,下列分式一定有意义的是( )
| A. | $\frac{{{a^2}+a}}{a}$ | B. | $\frac{a}{{{a^2}+1}}$ | C. | $\frac{a}{{{a^2}-1}}$ | D. | $\frac{1}{{{a^2}-1}}$ |
1. 如图,已知DE∥BC,AD=2,BD=3,则△ADE和△ABC的面积比是( )
如图,已知DE∥BC,AD=2,BD=3,则△ADE和△ABC的面积比是( )
 如图,已知DE∥BC,AD=2,BD=3,则△ADE和△ABC的面积比是( )
如图,已知DE∥BC,AD=2,BD=3,则△ADE和△ABC的面积比是( )| A. | 2:3 | B. | 2:5 | C. | 4:9 | D. | 4:25 |
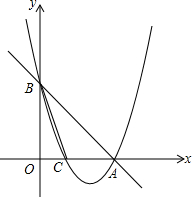 已知:如图直线y=-x+6与x轴、y轴分别交于A、B两点.抛物线y=$\frac{1}{2}$x2+bx+c过A、B两点,与x轴的另一个交点为C点.
已知:如图直线y=-x+6与x轴、y轴分别交于A、B两点.抛物线y=$\frac{1}{2}$x2+bx+c过A、B两点,与x轴的另一个交点为C点.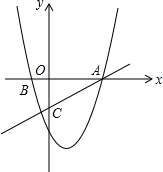 如图.在平面直角坐标系xOy中,抛物线y=x2-2x-3交x轴于A、B两点,直线y=$\frac{1}{3}$x-1交y轴于点C,若x轴上的点P满足PA=PC,则P点坐标为($\frac{4}{3},0$);若在抛物线对称轴上且位于x轴上方的点Q满足∠OAC<∠QCA<3∠OAC,则点Q纵坐标y取值范围为$0<y<\frac{17}{7}$.
如图.在平面直角坐标系xOy中,抛物线y=x2-2x-3交x轴于A、B两点,直线y=$\frac{1}{3}$x-1交y轴于点C,若x轴上的点P满足PA=PC,则P点坐标为($\frac{4}{3},0$);若在抛物线对称轴上且位于x轴上方的点Q满足∠OAC<∠QCA<3∠OAC,则点Q纵坐标y取值范围为$0<y<\frac{17}{7}$. 求出下列图中x的值.
求出下列图中x的值.