题目内容
1．
如图，已知DE∥BC，AD=2，BD=3，则△ADE和△ABC的面积比是（ ）| A． | 2：3 | B． | 2：5 | C． | 4：9 | D． | 4：25 |
分析 根据相似三角形的判定推出∠ADE∽△ABC，根据相似三角形的性质得出$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=（$\frac{AD}{AB}$）2，代入求出即可．
解答 解：∵DE∥BC，
∴∠ADE∽△ABC，
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=（$\frac{AD}{AB}$）2，
∵AD=2，BD=3，
∴AB=5，
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=（$\frac{AD}{AB}$）2=（$\frac{2}{5}$）2=$\frac{4}{25}$，
故选D．
点评 本题考查了相似三角形的性质和判定的应用，解此题的关键是能推出∠ADE∽△ABC，注意：相似三角形的面积比等于相似比的平方，难度适中．
练习册系列答案
相关题目
如图，在△ABD和△CDB中，AD=CB，AB、CD相交于点O，请你补充一个条件，使得△AOD≌△COB．你补充的条件是∠A=∠C．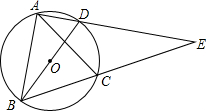
如图，BD是⊙O的直径，A、C是⊙O上的两点，且AB=AC，AD与BC的延长线交于点E．
如图，已知AD、BC相交于点O，AO=CO，BO=DO．求证：∠A=∠C．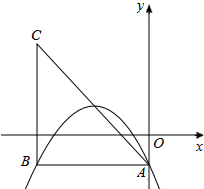
在平面直角坐标系中，已知抛物线y=ax2-2x+c（a，c为常数）的顶点为P，等腰直角三角形ABC的顶点A的坐标为（0，-1），C的坐标为（-4，3），直角顶点B在第二象限．
6．
如图，数轴上的点A和点B分别表示数a与数b，下列结论中正确的是（ ）
如图，数轴上的点A和点B分别表示数a与数b，下列结论中正确的是（ ）| A． | a＞b | B． | |a|＜|b| | C． | a＜-b | D． | a+b＜0 |