题目内容
2. 如图,△ABC中,点D、E分别在边AB、AC上,CD平分∠ACB,DE∥BC,若AC=12,AE=4,则BC=24.
如图,△ABC中,点D、E分别在边AB、AC上,CD平分∠ACB,DE∥BC,若AC=12,AE=4,则BC=24.
分析 先根据CD平分∠ACB,DE∥BC,求出△EDC是等腰三角形,即可求出DE的值,再根据DE∥BC,求出△ADE∽△ABC,然后根据相似三角形对应边成比例求解即可.
解答 解:∵CD平分∠ACB,
∴∠ECD=∠DCB,
又∵DE∥BC,
∴∠EDC=∠DCB,
∴∠EDC=∠ECD,
∴△EDC是等腰三角形.
即ED=EC=AC-AE=12-4=8.
∵DE∥BC,
∴△ADE∽△ABC,
∴DE:BC=AE:AC=4:12=1:3,
∴BC=3×8÷1=24.
故答案为:24.
点评 本题考查了相似三角形的判定与性质,解答本题的关键在于根据CD平分∠ACB,DE∥BC,求出△EDC是等腰三角形,△ADE∽△ABC,然后根据相似三角形对应边成比例求解.

练习册系列答案
相关题目
11.2016年10月26日,湖南永州梳子铺乡中学的全校学生在班主任和指导老师的带领下赶赴劳动实施基地,在班级分管的责任区开展实践劳动,该校七年级(2)班的同学在进行劳动前需要分成x组,若每小组分配11人,则余下1人,若每组12人,则有一组少4人,若每组分配7人时,则该班可分成( )
| A. | 7组 | B. | 8组 | C. | 9组 | D. | 10组 |
12.下列图形中是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |   |
 如图,小强告诉小华图中A、B两点的坐标分别为(-3,5)、(3,5),聪明的小华一下子说出了点C的坐标是(-1,7).
如图,小强告诉小华图中A、B两点的坐标分别为(-3,5)、(3,5),聪明的小华一下子说出了点C的坐标是(-1,7).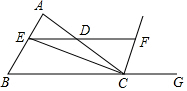 如图所示,CE为△ABC中∠BCA的角平分线,过E作BC的平行线交AC于点D,交∠ACG的平分线于点F,探究DE与DF之间的关系,并说明理由.
如图所示,CE为△ABC中∠BCA的角平分线,过E作BC的平行线交AC于点D,交∠ACG的平分线于点F,探究DE与DF之间的关系,并说明理由.