题目内容
17.解下列方程:(1)2x=5x-21;
(2)$\frac{x+1}{2}$=$\frac{4}{3}$x+1;
(3)$\frac{x-2}{0.2}$-$\frac{x+1}{0.5}$=3;
(4)|x-5|=2;
(5)x-3=4-$\frac{1}{2}$x;
(6)$\frac{1}{3}$(2x-5)=$\frac{1}{4}$(x-3)-$\frac{1}{12}$.
分析 (1)方程移项合并,把x系数化为1,即可求出解;
(2)方程去分母,去括号,移项合并,把x系数化为1,即可求出解;
(3)方程整理后,去分母,去括号,移项合并,把x系数化为1,即可求出解;
(4)方程利用绝对值的代数意义化简,求出解即可;
(5)方程去分母,去括号,移项合并,把x系数化为1,即可求出解;
(6)方程去分母,去括号,移项合并,把x系数化为1,即可求出解.
解答 解:(1)方程移项合并得:-3x=-21,
解得:x=7;
(2)去分母得:3x+3=8x+6,
移项合并得:5x=-3,
解得:x=-0.6;
(3)方程整理得:$\frac{10x-20}{2}$-$\frac{10x+10}{5}$=3,即5x-10-2x-2=3,
移项合并得:3x=15,
解得:x=5;
(4)方程变形得:x-5=2或x-5=-2,
解得:x=7或3;
(5)去分母得:2x-6=8-x,
移项合并得:3x=14,
解得:x=$\frac{14}{3}$;
(6)去分母得:4(2x-5)=3(x-3)-1,
去括号得:8x-20=3x-9-1,
移项合并得:5x=10,
解得:x=2.
点评 此题考查了解一元一次方程,其步骤为:去分母,去括号,移项合并,把未知数系数化为1,求出解.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
9.为了加强公民的节水意识,合理利用水资源,某市采用价格调控手段达到节水目的,该市自来水收费价目表,如图所示,
(1)若该用户1月用水9m3,则应收水费24元;
(2)若该用户2月缴水费48元;求该用户2月用多少立方米的水?
(3)若该户居民3、4月份共用水15m3(4月份用水量超过3月份),共交水费44元,则该居民3、4各月份用水多少立方米?
| 价目表 | |
| 每月用水量 | 单价 |
| 不超出6m3的部分 | 2元/m3 |
| 超出6m3不超出10m3的部分 | 4元/m3 |
| 超出10m3的部分 | 8元/m3 |
| 注:消费按月结算 | |
(2)若该用户2月缴水费48元;求该用户2月用多少立方米的水?
(3)若该户居民3、4月份共用水15m3(4月份用水量超过3月份),共交水费44元,则该居民3、4各月份用水多少立方米?
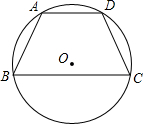 如图,四边形ABCD内接于⊙O,AD∥BC,求证:AB=CD.
如图,四边形ABCD内接于⊙O,AD∥BC,求证:AB=CD.