题目内容
为了充分利用课程资源,某校组织学生从学校出发,步行6千米到科技展览馆参观,返回时比去时每小时少走1千米,结果返回时比去时多用了半小时,则学生返回时步行的速度为 .
考点:分式方程的应用
专题:
分析:设学生返回时步行的速度为x千米/时,所以根据返回时比去时每小题少走1千米得到去的时候的速度为(x+1)千米/时,然后利用返回时比去时多用了半小时即可列出方程
-
=
,解方程就可以求出学生返回时步行的速度.
| 6 |
| x |
| 6 |
| x+1 |
| 1 |
| 2 |
解答:解:设学生返回时步行的速度为x千米/时,
根据题意得
-
=
,
整理,得x2+x-12=0,
解得x1=3,x2=-4,
经检验,x1=3,x2=-4都是原方程的根,
但x2=-4不符合题意,舍去,
∴x=3.即学生返回时步行的速度为3千米/时.
故答案为:3千米/时.
根据题意得
| 6 |
| x |
| 6 |
| x+1 |
| 1 |
| 2 |
整理,得x2+x-12=0,
解得x1=3,x2=-4,
经检验,x1=3,x2=-4都是原方程的根,
但x2=-4不符合题意,舍去,
∴x=3.即学生返回时步行的速度为3千米/时.
故答案为:3千米/时.
点评:此题是一个行程问题,主要考查利用路程=速度×时间来列出方程.分析题意,找到关键描述语,找到合适的等量关系是解决问题的关键.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
 有理数a,b,c在数轴上对应的点如图所示,则下面式子中正确的是( )
有理数a,b,c在数轴上对应的点如图所示,则下面式子中正确的是( )| A、c+b>a+b |
| B、ac>ab |
| C、cb<ab |
| D、cb>ab |
已知两圆的半径分别为10和6,圆心距为3,则这两圆的位置关系是( )
| A、外离 | B、外切 | C、相交 | D、内含 |
 如图,EF∥GH,点A在EF上,AP,AQ分别交GH于点B、C,且AP⊥AQ,∠PBG=35°,则∠FAC=
如图,EF∥GH,点A在EF上,AP,AQ分别交GH于点B、C,且AP⊥AQ,∠PBG=35°,则∠FAC= 如图,点A在x轴正半轴上,OA=2,∠AOB=30°,∠ABO=45°.
如图,点A在x轴正半轴上,OA=2,∠AOB=30°,∠ABO=45°.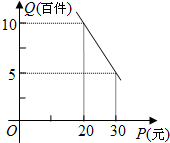 单价P(元)的关系如图所示;维持企业的正常运转每月需最低生活费外的各种开支2000元.
单价P(元)的关系如图所示;维持企业的正常运转每月需最低生活费外的各种开支2000元.