题目内容
17.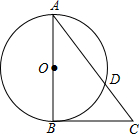 如图,△ABC是Rt△,∠ABC=90°,以AB为直径的⊙O交AC于D,⊙O的半径为5,$tanA=\frac{3}{4}$.
如图,△ABC是Rt△,∠ABC=90°,以AB为直径的⊙O交AC于D,⊙O的半径为5,$tanA=\frac{3}{4}$.(1)利用尺规作图,过点D作⊙O的切线DE,交BC于点E,保留作图痕迹;
(2)求线段CD的长.
分析 (1)连接OD,作∠BOD的平分线交BC于点E,连接DE,DE就是⊙O的切线.
(2)连接BD,只要证明△ABD~△ACB,得$\frac{AD}{AB}$=$\frac{AB}{AC}$,求出AC即可解决问题.
解答 解:(1)如图,连接OD,作∠BOD的平分线交BC于点E,连接DE,DE就是⊙O的切线.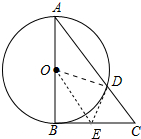
(2)连接BD,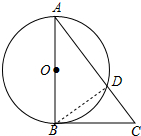
∵BD是直径,
∴∠ADB=90°,
∵$tanA=\frac{3}{4}$.AB=10,
∴AD=8,BD=6,
∵∠BAD=∠BAC,∠ABC=∠ADB=90°,
∴△ABD~△ACB
∴$\frac{AD}{AB}$=$\frac{AB}{AC}$,
∴AC=$\frac{25}{2}$,
∴CD=AC-AD=$\frac{9}{2}$.
点评 本题考查切线的性质、解直角三角形、相似三角形的判定和性质等知识,解题的关键是学会添加辅助线,构造相似三角形解决问题,属于中考常考题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10. 小明“六、一”去公园玩投掷飞镖的游戏,投中国中阴影部分由奖品(飞镖盘被平均分成8份),小明一次投镖能获得奖品的概率是( )
小明“六、一”去公园玩投掷飞镖的游戏,投中国中阴影部分由奖品(飞镖盘被平均分成8份),小明一次投镖能获得奖品的概率是( )
 小明“六、一”去公园玩投掷飞镖的游戏,投中国中阴影部分由奖品(飞镖盘被平均分成8份),小明一次投镖能获得奖品的概率是( )
小明“六、一”去公园玩投掷飞镖的游戏,投中国中阴影部分由奖品(飞镖盘被平均分成8份),小明一次投镖能获得奖品的概率是( )| A. | $\frac{1}{8}$ | B. | $\frac{3}{8}$ | C. | $\frac{8}{8}$ | D. | $\frac{1}{2}$ |
8.二次函数y=x2+2x+m(m为常数)的图象与x轴交点A(x1,0),B(x2,0),且x1<x2<0,已知当x=a时,y<0,那么当x=a+2时,函数值( )
| A. | y<m | B. | y>m | C. | y=m | D. | 无法确定 |
5.下列图形是中心对称图形但不是轴对称图形的是( )
| A. | 菱形 | B. | 矩形 | C. | 正三角形 | D. | 平行四边形 |
2. 我市正在进行轻轨九号线的建设,为了缓解市区一些主要路段的交通拥堵现状,交警大队在主要路口设置了交通路况指示牌如图所示,小明在离指示牌3米的点A处测得指示牌顶端D点和底端E点的仰角分别为60°和30°,则路况指示牌DE的高度为( )
我市正在进行轻轨九号线的建设,为了缓解市区一些主要路段的交通拥堵现状,交警大队在主要路口设置了交通路况指示牌如图所示,小明在离指示牌3米的点A处测得指示牌顶端D点和底端E点的仰角分别为60°和30°,则路况指示牌DE的高度为( )
 我市正在进行轻轨九号线的建设,为了缓解市区一些主要路段的交通拥堵现状,交警大队在主要路口设置了交通路况指示牌如图所示,小明在离指示牌3米的点A处测得指示牌顶端D点和底端E点的仰角分别为60°和30°,则路况指示牌DE的高度为( )
我市正在进行轻轨九号线的建设,为了缓解市区一些主要路段的交通拥堵现状,交警大队在主要路口设置了交通路况指示牌如图所示,小明在离指示牌3米的点A处测得指示牌顶端D点和底端E点的仰角分别为60°和30°,则路况指示牌DE的高度为( )| A. | 3-$\sqrt{3}$ | B. | 2$\sqrt{3}$-3 | C. | 2$\sqrt{3}$ | D. | 3+$\sqrt{3}$ |
9.小明到眼镜店调查了近视眼镜镜片的度数和镜片焦距的关系,发现镜片的度数y(度)是镜片焦距x(厘米)(x>0)的反比例函数,调查数据如表:
(1)求y与x的函数表达式;
(2)若小明所戴近视眼镜镜片的度数为500度,求该镜片的焦距.
| 眼镜片度数y(度) | 400 | 625 | 800 | 1000 | 1250 | … |
| 镜片焦距x(厘米) | 25 | 16 | 12.5 | 10 | 8 | … |
(2)若小明所戴近视眼镜镜片的度数为500度,求该镜片的焦距.
 如图,在Rt△ABC中,∠C=90°,AC=8m,BC=6m,点P由C点出发以2m/s的速度向终点A匀速移动,同时点Q由点B出发以1m/s的速度向终点C匀速移动,当一个点到达终点时另一个点也随之停止移动.
如图,在Rt△ABC中,∠C=90°,AC=8m,BC=6m,点P由C点出发以2m/s的速度向终点A匀速移动,同时点Q由点B出发以1m/s的速度向终点C匀速移动,当一个点到达终点时另一个点也随之停止移动. 如图,在直角坐标系中.
如图,在直角坐标系中.