题目内容
8.二次函数y=x2+2x+m(m为常数)的图象与x轴交点A(x1,0),B(x2,0),且x1<x2<0,已知当x=a时,y<0,那么当x=a+2时,函数值( )| A. | y<m | B. | y>m | C. | y=m | D. | 无法确定 |
分析 将解析式配方成顶点式,可知其对称轴为x=-1,结合抛物线与x轴的交点横坐标x1<x2<0得x1+2>0,再根据当x=a时y<0即a>x1,从而可得a+2>x1+2>0,即可得答案.
解答 解:∵y=x2+2x+m=(x+1)2+m-1,
∴抛物线的开口向上,对称轴为x=-1,
由抛物线与x轴交点A(x1,0),B(x2,0),且x1<x2<0,
则抛物线的图象如图:
∴x1>-2,即x1+2>0,
∵当x=a时,y<0,
∴a>x1,
∴a+2>x1+2>0,
∴当x=a+2时,函数值y>m,
故选:B.
点评 本题主要考查二次函数与x轴交点问题,根据抛物线对称轴与及抛物线与x轴交点横坐标的大小判断出x1+2>0是解题的关键.

练习册系列答案
 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
1.函数y=$\frac{x+2}{x-5}$中自变量x的取值范围是( )
| A. | x>5 | B. | x<5 | C. | x≠5 | D. | x=5 |
19.下列调查中,调查方式选择合理的是( )
| A. | 了解妫水河的水质情况,选择抽样调查 | |
| B. | 了解某种型号节能灯的使用寿命,选择全面调查 | |
| C. | 了解一架Y-8GX7新型战斗机各零部件的质量,选择抽样调查 | |
| D. | 了解一批药品是否合格,选择全面调查 |
3.在下列交通标志中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
13.在等边三角形、正方形、菱形和等腰梯形中,是中心对称图形的个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 如图,△ABC经过平移得到△A1B1C1,B1C=6cm,BC=3.5cm,则BC1=1cm;若∠B1=90°,∠A=60°,则∠A1C1B1=30°.
如图,△ABC经过平移得到△A1B1C1,B1C=6cm,BC=3.5cm,则BC1=1cm;若∠B1=90°,∠A=60°,则∠A1C1B1=30°.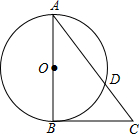 如图,△ABC是Rt△,∠ABC=90°,以AB为直径的⊙O交AC于D,⊙O的半径为5,$tanA=\frac{3}{4}$.
如图,△ABC是Rt△,∠ABC=90°,以AB为直径的⊙O交AC于D,⊙O的半径为5,$tanA=\frac{3}{4}$. 如图,P为正方形ABCD的边BC上一动点(点P与点B,C不重合),连接AP,过点B作BQ⊥AP交CD于点Q,将△BQC沿BQ所在的直线对折得到△BQC′,延长QC′交BA的延长线于点M.
如图,P为正方形ABCD的边BC上一动点(点P与点B,C不重合),连接AP,过点B作BQ⊥AP交CD于点Q,将△BQC沿BQ所在的直线对折得到△BQC′,延长QC′交BA的延长线于点M.