题目内容
4. 如图,直线EF与MN相交于点O,∠MOE=30°,将一直角三角尺的直角顶点与O重合,直角边OA与MN重合,OB在∠NOE内部.操作:将三角尺绕点O以每秒3°的速度沿顺指针方向旋转一周,设运动时间为t(s).
如图,直线EF与MN相交于点O,∠MOE=30°,将一直角三角尺的直角顶点与O重合,直角边OA与MN重合,OB在∠NOE内部.操作:将三角尺绕点O以每秒3°的速度沿顺指针方向旋转一周,设运动时间为t(s).(1)当t为何值时,直角边OB恰好平分∠NOE?此时OA是否平分∠MOE?请说明理由;
(2)若在三角尺转动的同时,直线EF也绕点O以每秒9°的速度顺时针方向旋转一周,当一方先完成旋转一周时,另一方同时停止转动.
①当t为何值时,EF平分∠AOB?
②EF能否平分∠NOB?若能请直接写出t的值;若不能,请说明理由.
分析 (1)根据:角度=速度×时间进行计算,由等量关系:直角边OB恰好平分∠NOE,列出方程求解即可.
(2)①由于OE的旋转速度快,需要考虑2种情形列方程解决.
②通过计算分析,OE,OB的位置,需要考虑2种情形列方程解决.
解答 解:(1)∵当直角边OB恰好平分∠NOE时,∠NOB=$\frac{1}{2}$∠NOE=$\frac{1}{2}$(180°-30°)=75°,
∴90°-3t°=75°,
解得:t=5.
此时∠MOA=3°×5=15°=$\frac{1}{2}$∠MOE,
∴此时OA平分∠MOE.
(2)①OE平分∠AOB,
依题意有30°+9t-3t=90°÷2,
解得t=2.5;
OF平分∠AOB,
依题意有30°+9t-3t=180°+90°÷2,
解得t=32.5.
故当t为2.5s或32.5s时,EF平分∠AOB
②OB在MN上面,
依题意有180°-30°-9t=(90°-3t)÷2,
解得t=14;
OB在MN下面,
依题意有9t-(360°-30°)=(3t-90°)÷2,
解得t=38.
故EF能平分∠NOB,t的值为14s或38s.
点评 本题目考查了角平分线的定义,旋转的速度,角度,时间的关系,应用方程的思想是解决问题的关键,还需要通过计算进行初步估计位置,掌握分类思想,注意不能漏解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,点A在双曲线y=$\frac{k}{x}$(x>0)上,点B在直线y=-0.5x+5上,
如图,点A在双曲线y=$\frac{k}{x}$(x>0)上,点B在直线y=-0.5x+5上,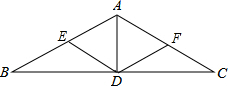 如图,在△ABC中,AB=AC,∠BAC=120°,AD是BC边的中线,点E、F分别是AB、AC的中点,连接DE、DF.
如图,在△ABC中,AB=AC,∠BAC=120°,AD是BC边的中线,点E、F分别是AB、AC的中点,连接DE、DF. 已知,如图△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,求证:①BF=AC;②BF=2CE.
已知,如图△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,求证:①BF=AC;②BF=2CE.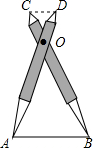 如图,比例规是一种画图工具,它由长度相等的两脚AD和BC交叉构成,利用它可以把线段按一定的比例伸长或缩短,如果把比例规的两脚合上,使螺丝钉固定在刻度3的地方(即同时使OA=3OD,OB=3OC),然后张开两脚,使A、B两个尖端分别在线段l的两个端点上,若CD=3.2cm,则AB的长为9.6cm.
如图,比例规是一种画图工具,它由长度相等的两脚AD和BC交叉构成,利用它可以把线段按一定的比例伸长或缩短,如果把比例规的两脚合上,使螺丝钉固定在刻度3的地方(即同时使OA=3OD,OB=3OC),然后张开两脚,使A、B两个尖端分别在线段l的两个端点上,若CD=3.2cm,则AB的长为9.6cm.