题目内容
12.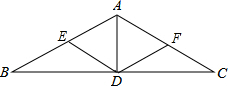 如图,在△ABC中,AB=AC,∠BAC=120°,AD是BC边的中线,点E、F分别是AB、AC的中点,连接DE、DF.
如图,在△ABC中,AB=AC,∠BAC=120°,AD是BC边的中线,点E、F分别是AB、AC的中点,连接DE、DF.(1)求证:△AED是等边三角形;
(2)若AB=2,则四边形AEDF的周长是4.
分析 (1)根据等腰三角形的性质得到∠B=∠C=30°,AD⊥BC,根据直角三角形的性质得到AD=$\frac{1}{2}$AB,于是得到结论;
(2)根据菱形的判定得到四边形AEDF是菱形,于是得到结论.
解答 (1)证明:∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°,
∵AD是BC边的中线,
∴AD⊥BC,
∴∠BAD=60°,
∴AD=$\frac{1}{2}$AB,
∵AE=$\frac{1}{2}$AB,
∴AE=AD,
∴△ADE是等边三角形;
(2)解:由(1)证得△ADE是等边三角形,同理△ADF是等边三角形,
∴AE=AF=AD=DE=DF,
∴四边形AEDF是菱形,
∵AE=$\frac{1}{2}$AB=1,
∴四边形AEDF的周长是4,
故答案为:4.
点评 本题考查了含30°角的直角三角形的性质,等腰三角形的性质,等边三角形的判定和性质,正确的识别图形是解题的关键.

练习册系列答案
相关题目
17.代数式:$\frac{ab}{bc}$,-4x,-$\frac{2}{3abc}$,π,$\frac{2a-1}{3}$,x+$\frac{5}{y}$,0,$\frac{-a{b}^{2}}{π}$,a2-b2中,单项式和多项式分别有( )
| A. | 5个,1个 | B. | 5个,2个 | C. | 4个,1个 | D. | 4个,2个 |
1. 平顶山市积极开展“节水”活动,小明利用课余时间对某小区 300户居民的用 水情况进行统计,发现12月份各户居民的用水量比11月份有所下降,小明将12月份各户居民的节水量统汁整理成如下统计图表:
平顶山市积极开展“节水”活动,小明利用课余时间对某小区 300户居民的用 水情况进行统计,发现12月份各户居民的用水量比11月份有所下降,小明将12月份各户居民的节水量统汁整理成如下统计图表:
(1)300户居民12月份节水量的众数、中位数分别是多少?
(2)扇形面积统计图中2.5吨对应扇形的圆心角为多少度?
(3)该小区300户居民12只份平均每户节约用水多少吨?
 平顶山市积极开展“节水”活动,小明利用课余时间对某小区 300户居民的用 水情况进行统计,发现12月份各户居民的用水量比11月份有所下降,小明将12月份各户居民的节水量统汁整理成如下统计图表:
平顶山市积极开展“节水”活动,小明利用课余时间对某小区 300户居民的用 水情况进行统计,发现12月份各户居民的用水量比11月份有所下降,小明将12月份各户居民的节水量统汁整理成如下统计图表:| 节水量(吨) | 1 | 1.5 | 2.5 | 3 |
| 户数 | 50 | 80 | 100 | 70 |
(2)扇形面积统计图中2.5吨对应扇形的圆心角为多少度?
(3)该小区300户居民12只份平均每户节约用水多少吨?
 如图,⊙O的半径为r.A,B为⊙O上的两个不同点;以B为圆心.BA为半径的圆交⊙O于另一点C.P为⊙O内一点,使得△PAB为正三角形,CP交⊙O于另一点Q.
如图,⊙O的半径为r.A,B为⊙O上的两个不同点;以B为圆心.BA为半径的圆交⊙O于另一点C.P为⊙O内一点,使得△PAB为正三角形,CP交⊙O于另一点Q. 如图,直线EF与MN相交于点O,∠MOE=30°,将一直角三角尺的直角顶点与O重合,直角边OA与MN重合,OB在∠NOE内部.操作:将三角尺绕点O以每秒3°的速度沿顺指针方向旋转一周,设运动时间为t(s).
如图,直线EF与MN相交于点O,∠MOE=30°,将一直角三角尺的直角顶点与O重合,直角边OA与MN重合,OB在∠NOE内部.操作:将三角尺绕点O以每秒3°的速度沿顺指针方向旋转一周,设运动时间为t(s).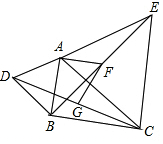 如图,在△ABC中,分别以AB,AC为边向外作△ABD和△ACE,且AD=AB,AE=AC,∠BAD=∠CAE,连接DC,BE,点G,F分别是DC,BE的中点,连接AF,FG.
如图,在△ABC中,分别以AB,AC为边向外作△ABD和△ACE,且AD=AB,AE=AC,∠BAD=∠CAE,连接DC,BE,点G,F分别是DC,BE的中点,连接AF,FG.