题目内容
1. 如图,⊙O与△ADE各边所在的直线分别相切于B、F、C,DE⊥AE,AD=10,AE=6.
如图,⊙O与△ADE各边所在的直线分别相切于B、F、C,DE⊥AE,AD=10,AE=6.(1)求BE+CD的值;
(2)求⊙O的半径r.
分析 (1)连接OF,OB,得到四边形OFEB是正方形,由O与△ADE各边所在的直线分别相切于B、F、C,得到CD=DF,EF=BE,于是得到结论;
(2)设圆的半径是x,则EF=BE=x,设DF=y,则DF=CD=y.根据勾股定理得到DE=$\sqrt{A{D}^{2}-A{E}^{2}}$=6,解方程组即可得到结论.
解答 解:(1)连接OF,OB,
则四边形OFEB是正方形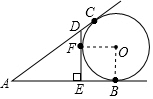 ,
,
∵O与△ADE各边所在的直线分别相切于B、F、C,
∴CD=DF,EF=BE,
∴DE=DF+EF=CD+BE=8;
(2)设圆的半径是x,则EF=BE=x,设DF=y,则DF=CD=y.
在直角△ADE中,DE=$\sqrt{A{D}^{2}-A{E}^{2}}$=8,
则x+y=8,10+y=6$\left\{\begin{array}{l}{x+y=8}\\{10+y=6+x}\end{array}\right.$x,
解方程组:$\left\{\begin{array}{l}{x=6}\\{y=2}\end{array}\right.$;$\left\{\begin{array}{l}{x+y=8}\\{10+y=6+x}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=6}\\{y=2}\end{array}\right.$.
即⊙O的半径是6.
点评 本题考查了切线长定理以及勾股定理的应用,正确列出方程是关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
11.$\frac{{a}^{2}+a-2}{{a}^{2}+3a+2}$•5(a+1)2等于( )
| A. | a2+2a+1 | B. | 5a2+10 a+5 | C. | 5a2-1 | D. | 5a2-5 |
16.下列计算正确的是( )
| A. | 5a+2a=7a2 | B. | 5a-2a=3 | C. | 5a-2a=3a | D. | -ab+2ab2=ab2 |
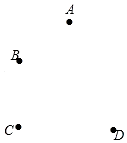 如图,平面上四个点A,B,C,D.按要求完成下列问题:
如图,平面上四个点A,B,C,D.按要求完成下列问题: