题目内容
3.先化简,再求值:$\frac{x}{{x}^{2}-2x+1}$÷(1+$\frac{x+1}{{x}^{2}-1}$),其中x=$\frac{1}{3}$.分析 原式括号中两项通分并利用同分母分式的加法法则计算,同时利用除法法则变形,约分得到最简结果,把x的值代入计算即可求出值.
解答 解:原式=$\frac{x}{(x-1)^{2}}$÷$\frac{{x}^{2}-1+x+1}{{x}^{2}-1}$=$\frac{x}{(x-1)^{2}}$•$\frac{(x+1)(x-1)}{x(x+1)}$=$\frac{1}{x-1}$,
当x=$\frac{1}{3}$时,原式=$\frac{1}{{\frac{1}{3}-1}}$=-$\frac{3}{2}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
14.2017的绝对值是( )
| A. | -2017 | B. | 2017 | C. | $\frac{1}{2017}$ | D. | -$\frac{1}{2017}$ |
18.下列运算中,计算结果不等于x6的是( )
| A. | x2•x4 | B. | x3+x3 | C. | x4÷x-2 | D. | (-x3)2 |
8.将二次函数y=x2的图象向左平移1个单位,则平移后的二次函数的解析式为( )
| A. | y=x2-1 | B. | y=x2+1 | C. | y=(x-1)2 | D. | y=(x+1)2 |
13.某商场为提高彩电销售人员的积极性,制订了新的工资分配方案,方案规定:每位销售人员的工资总额=基本工资+奖励工资,每位销售人员的月销售额为20000元,在销售定额内,得基本工资2000元.超过销售定额,超过部分的销售额按相应比例作为奖励工资,奖励工资发放比例表1所示.
表1:
表2:
(1)已知销售员甲本月领到的工资总额为2900元,请问销售员甲本月销售额是多少元?
(2)依法纳税是每个公民应尽的义务.根据我国税法规定,全月工资总额不超过3500元不必缴纳个人所得税;超过3500元的部分为“全月应纳税所得额”,表2是缴纳个人所得税率表.若销售员乙本月销售A、B两种型号的彩电15台,缴纳个人所得税后实际得到的工资为4858元.又知A型彩电的销售价为每台400元,B型彩电的销售价为每台6000元,请问销售员乙本月销售A型彩电多少台?
表1:
| 销售额 | 奖励工资比例 |
| 超过20000元但不超过30000部分 | 3% |
| 超过30000元但不超过50000部分 | 5% |
| 50000元以上的部分 | 8% |
| 全月应纳税所得额 | 税率 |
| 不超过1500元部分 | 3% |
| 超过1500元至4500元部分 | 10% |
| … | … |
(2)依法纳税是每个公民应尽的义务.根据我国税法规定,全月工资总额不超过3500元不必缴纳个人所得税;超过3500元的部分为“全月应纳税所得额”,表2是缴纳个人所得税率表.若销售员乙本月销售A、B两种型号的彩电15台,缴纳个人所得税后实际得到的工资为4858元.又知A型彩电的销售价为每台400元,B型彩电的销售价为每台6000元,请问销售员乙本月销售A型彩电多少台?
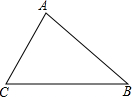 在△ABC中,∠C>∠B,BC边上的高AD交BC于点D,∠BAC的角平分线AE交BC于点E.
在△ABC中,∠C>∠B,BC边上的高AD交BC于点D,∠BAC的角平分线AE交BC于点E.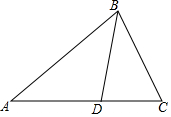 已知:如图,在△ABC中,D是AC上一点,$\frac{CB}{CD}$=$\frac{CA}{CB}$=$\frac{3}{2}$,△BCD的周长是24cm.
已知:如图,在△ABC中,D是AC上一点,$\frac{CB}{CD}$=$\frac{CA}{CB}$=$\frac{3}{2}$,△BCD的周长是24cm.