题目内容
17. 如图,正方形ABCD的边长为2,MN∥BC分别交AB、CD于点M、N,在MN上任取两点P、Q,那么图中阴影部分的面积是2.
如图,正方形ABCD的边长为2,MN∥BC分别交AB、CD于点M、N,在MN上任取两点P、Q,那么图中阴影部分的面积是2.
分析 阴影部分的面积等于正方形的面积减去△AQD和△BCP的面积和.而两个三角形等底即为正方形的边长,它们的高的和等于正方形的边长,得出阴影部分的面积=正方形面积的一半即可.
解答 解:由图知,阴影部分的面积等于正方形的面积减去△AQD和△BCP的面积.
而点P到BC的距离与点Q到AD的距离的和等于正方形的边长,
即△AQD和△BCP的面积的和等于正方形的面积的一半,
故阴影部分的面积=$\frac{1}{2}$×22=2.
故答案为:2.
点评 本题考查正方形的性质,正方形的面积,三角形的面积公式灵活运用,注意图形的特点.

练习册系列答案
相关题目
7.$\sqrt{16}$的算术平方根是( )
| A. | 2 | B. | 4 | C. | ±2 | D. | ±4 |
8.公司有330台机器需要一次性运送到某地,计划租用甲、乙两种货车共8辆,已知每辆甲种货车一次最多运送机器45台、租车费用为400元,每辆乙种货车一次最多运送机器30台、租车费用为280元
(Ⅰ)设租用甲种货车x辆(x为非负整数),试填写表格.
表一:
表二:
(Ⅱ)给出能完成此项运送任务的最节省费用的租车方案,并说明理由.
(Ⅰ)设租用甲种货车x辆(x为非负整数),试填写表格.
表一:
| 租用甲种货车的数量/辆 | 3 | 7 | x |
| 租用的甲种货车最多运送机器的数量/台 | 135 | 315 | 45x |
| 租用的乙种货车最多运送机器的数量/台 | 150 | 30 | -30x+240 |
| 租用甲种货车的数量/辆 | 3 | 7 | x |
| 租用甲种货车的费用/元 | 1200 | 2800 | 400x |
| 租用乙种货车的费用/元 | 1400 | 280 | -280x+2240 |
5.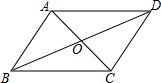 如图,平行四边形ABCD的对角线交于点O,且AB=6,△OCD的周长为19,则?ABCD的两条对角线的和是( )
如图,平行四边形ABCD的对角线交于点O,且AB=6,△OCD的周长为19,则?ABCD的两条对角线的和是( )
 如图,平行四边形ABCD的对角线交于点O,且AB=6,△OCD的周长为19,则?ABCD的两条对角线的和是( )
如图,平行四边形ABCD的对角线交于点O,且AB=6,△OCD的周长为19,则?ABCD的两条对角线的和是( )| A. | 13 | B. | 25 | C. | 26 | D. | 38 |
12.下列各组数中,不能构成直角三角形的是( )
| A. | 2,3,4 | B. | 5,12,13 | C. | 6,8,10 | D. | 3,4,5 |
2.已知菱形ABCD中,∠A=80°,下列结论正确的是( )
| A. | ∠B=80° | B. | ∠C=80° | C. | ∠D=80° | D. | 以上都错误 |
9.方程x2-3x+7=0的根的情况是( )
| A. | 没有实数根 | B. | 有无数个相等或不相等的实数根 | ||
| C. | 有两个不相等的实数根 | D. | 有两个相等的实数根 |