题目内容
关于x的方程x2+2kx+k-1=0的根的情况描述正确的是( )
| A、k为任何实数,方程都没有实数根 |
| B、k为任何实数,方程都有两个不相等的实数根 |
| C、k为任何实数,方程都有两个相等的实数根 |
| D、根据k的取值不同,方程根的情况分为没有实数根、有两个不相等的实数根和有两个相等的实数根三种 |
考点:根的判别式
专题:
分析:先计算判别式的值得到△=(2k-1)2+3,根据非负数的性质得△>0,然后根据判别式的意义进行判断.
解答:
解:△=4k2-4(k-1)
=(2k-1)2+3,
∵(2k-1)2≥0,
∴(2k-1)2+3>0,
即△>0,
∴方程有两个不相等的实数根.
故选B.
=(2k-1)2+3,
∵(2k-1)2≥0,
∴(2k-1)2+3>0,
即△>0,
∴方程有两个不相等的实数根.
故选B.
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
相关题目
式子
+
有意义的条件是( )
| -x |
| 1 |
| x+2 |
| A、x≥0 | B、x≤0且x≠-2 |
| C、x≠-2 | D、x≤0 |
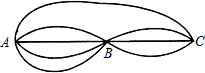 从A地到C地,可供选择的方案有走水路、走陆路、走空中.从A地到B地有2条水路、2条陆路,从B地到C地有3条陆路可供选择,走空中从A地不经B地直接到C地.则从A地到C地可供选择的方案有( )
从A地到C地,可供选择的方案有走水路、走陆路、走空中.从A地到B地有2条水路、2条陆路,从B地到C地有3条陆路可供选择,走空中从A地不经B地直接到C地.则从A地到C地可供选择的方案有( )| A、20种 | B、8种 | C、5种 | D、13 |
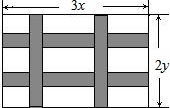 如图,要设计一幅长为3xcm,宽为2ycm的长方形图案,其中有两横两竖的彩条,横彩条的宽度均为acm,竖彩条的宽度均为bcm,则空白区域的面积是( )
如图,要设计一幅长为3xcm,宽为2ycm的长方形图案,其中有两横两竖的彩条,横彩条的宽度均为acm,竖彩条的宽度均为bcm,则空白区域的面积是( )| A、(6xy-6xa-4by+4ab)cm2 |
| B、(6xy+6xa+4by-4ab)cm2 |
| C、(6xy-6xb-4ay+4ab)cm2 |
| D、(6xy+6xb+4ay-4ab |
 如图,△ABC的边AB是⊙O的直径,⊙O与AC交于点D,∠BOD=90°,∠B=60°,则∠C=
如图,△ABC的边AB是⊙O的直径,⊙O与AC交于点D,∠BOD=90°,∠B=60°,则∠C= 已知,△ABC和△ECD都是等边三角形,且点B、C、D在一条直线上.
已知,△ABC和△ECD都是等边三角形,且点B、C、D在一条直线上.