题目内容
9.△ABC内接于⊙O中,OD⊥BC于D,若∠OBD=15°,则∠A=75°或105°.分析 如图1,圆心O在△ABC内,连接OB,OC,根据等腰三角形的性质得到∠ODB=90°,∠BOC=2∠BOD,根据三角形的内角和得到∠BOD=75°,根据圆周角定理即可得到结论;如图2,圆心O在△ABC外,连接OB,OC,设E是圆上的一点,连接BE,CE,根据等腰三角形的性质得到∠ODB=90°,∠BOC=2∠BOD,根据三角形的内角和得到∠BOD=75°,根据圆内接四边形的性质即可得到结论.
解答 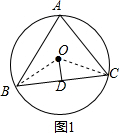 解:如图1,圆心O在△ABC内,连接OB,OC,
解:如图1,圆心O在△ABC内,连接OB,OC,
∴OB=OC,
∵OD⊥BC于D,
∴∠ODB=90°,∠BOC=2∠BOD,
∵∠OBD=15°,
∴∠BOD=75°,
∴∠BOC=150°,
∴∠A=$\frac{1}{2}∠$BOC=75°;
如图2,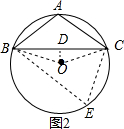 连接OB,OC,设E是圆上的一点,连接BE,CE,
连接OB,OC,设E是圆上的一点,连接BE,CE,
∴OB=OC,
∵OD⊥BC于D,
∴∠ODB=90°,∠BOC=2∠BOD,
∵∠OBD=15°,
∴∠BOD=75°,
∴∠BOC=150°,
∴∠E=$\frac{1}{2}∠$BOC=75°;
∴∠A=180°-∠E=105°,
综上所述:∠A=75°或105°.
故答案为:75°或105°.
点评 本题考查了圆周角定理,垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.

练习册系列答案
相关题目
4.如图,是一石拱桥的桥拱截面示意图,已知拱桥是一段优弧,桥拱顶到水面的距离CD为8m,桥拱半径OC为5m,则水面宽AB为( )


| A. | 8m | B. | 4m | C. | 6m | D. | 3m |
2.(a+b-c)(a-b-c)=[a+□][a-□],□里所填的各项分别是( )
| A. | b-c,b+c | B. | -b+c,b-c | C. | b-c,b-c | D. | -b+c,b+c |
3.若2x2y1-2m和3xn-1y2是同类项,则mn的值是( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{8}$ | D. | -$\frac{1}{8}$ |
 如图,在△ABC中,∠C=90°,AC=8,BC=6,DE是△ABD的边AB上的高,且AD=$2\sqrt{5}$,BD=$4\sqrt{5}$.求:DE的长.
如图,在△ABC中,∠C=90°,AC=8,BC=6,DE是△ABD的边AB上的高,且AD=$2\sqrt{5}$,BD=$4\sqrt{5}$.求:DE的长. 如图是什么几何体的展开图?
如图是什么几何体的展开图?