题目内容
13. 河的一旁有两个村子A、B,要在河边建一水泵站引水到村里.一村民画了一张图,以直线l表示一条河,求作一点P,使P到A、B的距离和最短,作出P点,并用几何语言叙述你的理由.
河的一旁有两个村子A、B,要在河边建一水泵站引水到村里.一村民画了一张图,以直线l表示一条河,求作一点P,使P到A、B的距离和最短,作出P点,并用几何语言叙述你的理由.
分析 根据轴对称的性质,三角形三边关系定理判定线段的大小.
解答 解:如图所示:
理由:在直线l上任取一点Q,连接AQ、BQ,
∵A、C两点关于直线l轴对称,
∴AP=PC,AQ=CQ,CP+PB=BC,
又∵在△BCQ中,由三边关系定理,得BQ+CQ>BC,
即BQ+AQ>CP+BP,
∴BQ+CQ>AP+BP. 
点评 本题考查了三角形三边关系和最短线路问题.解题的关键是根据“三角形两边之和大于第三边”,判断AP+BP最小.

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
3.下列由2和3组成的四个算式中,值最小的是( )
| A. | 2-3 | B. | 2÷3 | C. | 23 | D. | 2-3 |
4.下列各数中,是有理数的是( )
| A. | $\root{3}{2}$ | B. | $-\sqrt{3}$ | C. | π | D. | $\frac{1}{3}$ |
1.请用下表中的数据填空:
(1)655.36的平方根是±25.6.
(2)$\sqrt{670.8}$=25.9.
(3)25.2<$\sqrt{640}$<25.3.
| x | 25 | 25.1 | 25.2 | 25.3 | 25.4 | 25.5 | 25.6 | 25.7 | 25.8 | 25.9 | 26 |
| x2 | 625 | 630.01 | 635.04 | 640.09 | 645.16 | 650.25 | 655.36 | 660.49 | 665.64 | 670.81 | 676 |
(2)$\sqrt{670.8}$=25.9.
(3)25.2<$\sqrt{640}$<25.3.
18.等腰三角形的底角是70°,则顶角为( )
| A. | 40° | B. | 70° | C. | 55° | D. | 45° |
3.下列实数是无理数的是( )
| A. | -1 | B. | 0 | C. | 3.14 | D. | $\sqrt{5}$ |
 已知:点A、E、D、C在同一条直线上,AE=CD,EF∥BD,EF=BD.求证:AB∥CF.
已知:点A、E、D、C在同一条直线上,AE=CD,EF∥BD,EF=BD.求证:AB∥CF.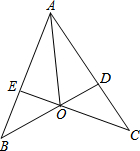 如图,BD⊥AC,CE⊥AB,垂足分别为D、E,BD与CE相交于点O,AO平分∠BAC.求证:OB=OC.
如图,BD⊥AC,CE⊥AB,垂足分别为D、E,BD与CE相交于点O,AO平分∠BAC.求证:OB=OC.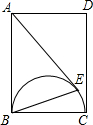 如图,在矩形ABCD中,AB=3,BC=2,以BC为直径在矩形内作半圆,自点A作半圆的切线AE,则$\frac{CE}{BC}$=$\frac{\sqrt{10}}{10}$.
如图,在矩形ABCD中,AB=3,BC=2,以BC为直径在矩形内作半圆,自点A作半圆的切线AE,则$\frac{CE}{BC}$=$\frac{\sqrt{10}}{10}$.