题目内容
8.(1)计算:($\sqrt{15}$-3)0-|-2|-(-$\frac{1}{2}$)-2+$\sqrt{(1-\sqrt{2})^{2}}$(2)解方程:x2-3x+1=0.
分析 (1)根据实数的混合运算顺序依次计算可得;
(2)公式法求解可得.
解答 解:(1)原式=$1-2-4+\sqrt{2}-1$=$-6+\sqrt{2}$;
(2)∵a=1,b=-3,c=1,
∴△=b2-4ac=9-4=5>0,
则x=$\frac{3±\sqrt{5}}{2}$,
${x_1}=\frac{{3+\sqrt{5}}}{2},{x_2}=\frac{{3-\sqrt{5}}}{2}$.
点评 本题主要考查解一元二次方程的能力和实数的混合运算,熟练掌握解一元二次方程的几种常用方法:直接开平方法、因式分解法、公式法、配方法,结合方程的特点选择合适、简便的方法是解题的关键.

练习册系列答案
相关题目
3.当-1≤x≤2时,二次函数y=x2+2mx+m+2,有最小值-3,则实数m的值为( )
| A. | $\frac{1+\sqrt{21}}{2}$或$\frac{1-\sqrt{21}}{2}$ | B. | 6或-$\frac{9}{5}$ | ||
| C. | 6或$\frac{1-\sqrt{21}}{2}$ | D. | 6或-$\frac{9}{5}$或$\frac{1-\sqrt{21}}{2}$或$\frac{1+\sqrt{21}}{2}$ |

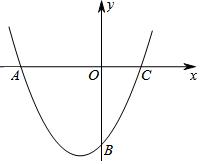 已知抛物线经过A(-4,0),B(0,-4),C(2,0)三点.
已知抛物线经过A(-4,0),B(0,-4),C(2,0)三点. 如图,已知等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为4厘米,BA与MN在同一直线上,开始时点A与点M重合,让△ABC向右移动,最后点A与点N重合.
如图,已知等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为4厘米,BA与MN在同一直线上,开始时点A与点M重合,让△ABC向右移动,最后点A与点N重合.