题目内容
13.已知抛物线y=ax2+bx+c(a≠0)与x轴交点为(-1,0)和(3,0),与y轴交点为(0,-2),则一元二次方程ax2+bx+c=0(a≠0)的根为( )| A. | x1=-1,x2=3 | B. | x1=-2,x2=3 | C. | x1=1,x2=-3 | D. | x1=-1,x2=-2 |
分析 根据抛物线与x轴的交点问题,两交点的横坐标即为方程ax2+bx+c=0的解.
解答 解:∵抛物线y=ax2+bx+c与x轴的两个交点分别为(-1,0),(3,0),
即自变量为-1和3时函数值为0,
∴一元二次方程ax2+bx+c=0的根为x1=-1,x2=3.
故选A.
点评 本题考查了抛物线与x轴的交点,关键是掌握求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标,令y=0,即ax2+bx+c=0,解关于x的一元二次方程即可求得交点横坐标.△=b2-4ac决定抛物线与x轴的交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
相关题目
6.已知方程3x+m=3-x的解为x=-1,则m的值为( )
| A. | 13 | B. | 7 | C. | -10 | D. | -13 |
4. 如图,OP是∠AOB的平分线,点C、D分别在∠AOB的两边OA、OB上,添加下列条件,不能判定△POC≌△POD的选项是( )
如图,OP是∠AOB的平分线,点C、D分别在∠AOB的两边OA、OB上,添加下列条件,不能判定△POC≌△POD的选项是( )
 如图,OP是∠AOB的平分线,点C、D分别在∠AOB的两边OA、OB上,添加下列条件,不能判定△POC≌△POD的选项是( )
如图,OP是∠AOB的平分线,点C、D分别在∠AOB的两边OA、OB上,添加下列条件,不能判定△POC≌△POD的选项是( )| A. | ∠OPC=∠OPD | B. | PC=PD | C. | PC⊥OA,PD⊥OB | D. | OC=OD |
18. 如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E且AB=6cm,则△DEB的周长为( )
如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E且AB=6cm,则△DEB的周长为( )
 如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E且AB=6cm,则△DEB的周长为( )
如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E且AB=6cm,则△DEB的周长为( )| A. | 40cm | B. | 6cm | C. | 8cm | D. | 10cm |
5.若扇形的圆心角为60°,半径为6,则该扇形的弧长为( )
| A. | π | B. | 2π | C. | 3π | D. | 4π |
2.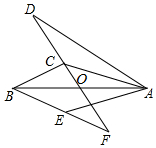 如图,△ABE和△ADC分别沿着边AB、AC翻折180°形成的,若∠BCA:∠ABC:∠BAC=28:5:3,BE与DC交于点F,则∠EFC的度数为( )
如图,△ABE和△ADC分别沿着边AB、AC翻折180°形成的,若∠BCA:∠ABC:∠BAC=28:5:3,BE与DC交于点F,则∠EFC的度数为( )
 如图,△ABE和△ADC分别沿着边AB、AC翻折180°形成的,若∠BCA:∠ABC:∠BAC=28:5:3,BE与DC交于点F,则∠EFC的度数为( )
如图,△ABE和△ADC分别沿着边AB、AC翻折180°形成的,若∠BCA:∠ABC:∠BAC=28:5:3,BE与DC交于点F,则∠EFC的度数为( )| A. | 20° | B. | 30° | C. | 40° | D. | 45° |
1.若三角形的三边长分别为a、b、c,满足a2b-a2c+b2c-b3=0,这个三角形是( )
| A. | 等腰三角形 | B. | 直角三角形 | ||
| C. | 等边三角形 | D. | 三角形的形状不确定 |