题目内容
2.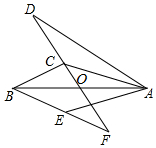 如图,△ABE和△ADC分别沿着边AB、AC翻折180°形成的,若∠BCA:∠ABC:∠BAC=28:5:3,BE与DC交于点F,则∠EFC的度数为( )
如图,△ABE和△ADC分别沿着边AB、AC翻折180°形成的,若∠BCA:∠ABC:∠BAC=28:5:3,BE与DC交于点F,则∠EFC的度数为( )| A. | 20° | B. | 30° | C. | 40° | D. | 45° |
分析 根据∠BCA:∠ABC:∠BAC=28:5:3,三角形的内角和定理分别求得∠BCA,∠ABC,∠BAC的度数,然后根据折叠的性质求出∠D、∠DAE、∠BEA的度数,在△AOD中,根据三角形的内角和定理求出∠AOD的度数,继而可求得∠EOF的度数,最后根据三角形的外角定理求出∠EFC的度数.
解答 解:在△ABC中,
∵∠BCA:∠ABC:∠BAC=28:5:3,
∴设∠BCA为28x,∠ABC为5x,∠BAC为3x,
则28x+5x+3x=180°,
解得:x=5°,
则∠BCA=140°,∠ABC=25°,∠BAC=15°,
由折叠的性质可得:∠D=25°,∠DAE=3∠BAC=45°,∠BEA=140°,
在△AOD中,∠AOD=180°-∠DAE-∠D=110°,
∴∠EOF=∠AOD=110°,
∴∠EFC=∠BEA-∠EOF=140°-110°=30°.
故选B.
点评 本题考查图形的折叠变化及三角形的内角和定理.关键是要理解折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,只是位置变化.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
13.已知抛物线y=ax2+bx+c(a≠0)与x轴交点为(-1,0)和(3,0),与y轴交点为(0,-2),则一元二次方程ax2+bx+c=0(a≠0)的根为( )
| A. | x1=-1,x2=3 | B. | x1=-2,x2=3 | C. | x1=1,x2=-3 | D. | x1=-1,x2=-2 |
7.下列说法正确的是( )
| A. | 有理数分为正数和负数 | B. | 有理数都有相反数 | ||
| C. | 倒数等于它本身的数只有一个 | D. | 若a为有理数,则-a一定是负数 |
 如图所示的正方形网格中,网格线的交点称为格点.已知A、B是两格点,如果C也是图中的格点,且使得△ABC为等腰三角形,则点C的个数是( )
如图所示的正方形网格中,网格线的交点称为格点.已知A、B是两格点,如果C也是图中的格点,且使得△ABC为等腰三角形,则点C的个数是( )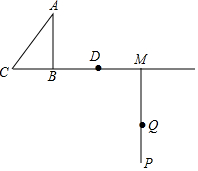 如图,Rt△ABC中,∠ABC=90°,AB=4,BC=3,点D从B点出发,沿射线CB方向以每秒3个单位长度的速度运动,射线MP⊥射线CB,且BM=10,点Q从M点出发,沿射线MQ方向以每秒a个单位长度的速度运动,己知D,Q两点同时出发,记时间为t.
如图,Rt△ABC中,∠ABC=90°,AB=4,BC=3,点D从B点出发,沿射线CB方向以每秒3个单位长度的速度运动,射线MP⊥射线CB,且BM=10,点Q从M点出发,沿射线MQ方向以每秒a个单位长度的速度运动,己知D,Q两点同时出发,记时间为t.