题目内容
如图，在Rt△ABC中，∠ACB=90°，AC=BC=2，以BC为直径的半圆交AB于点D，P是 |
| CD |
考点：勾股定理,线段的性质：两点之间线段最短,等腰直角三角形
专题：
分析：找到BC的中点E，连接AE，交半圆于P2，在半圆上取P1，连接AP1，EP1，可见，AP1+EP1＞AE，即AP2是AP的最小值，再根据勾股定理求出AE的长，然后减掉半径即可．
解答：
解：找到BC的中点E，连接AE，交半圆于P2，在半圆上取P1，连接AP1，EP1，
可见，AP1+EP1＞AE，
即AP2是AP的最小值，
∵AE=
=
，P2E=1，
∴AP2=
-1．
故答案为：
-1．
解：找到BC的中点E，连接AE，交半圆于P2，在半圆上取P1，连接AP1，EP1，可见，AP1+EP1＞AE，
即AP2是AP的最小值，
∵AE=
| 22+12 |
| 5 |
∴AP2=
| 5 |
故答案为：
| 5 |
点评：本题考查了勾股定理、最短路径问题，利用两点之间线段最短是解题的关键．
练习册系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
如图，已知在△ABC中，AD平分∠EAC且AD∥BC，那么∠B=∠C吗？请说明理由．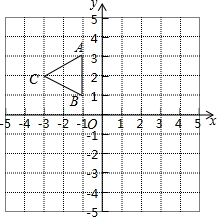
如图，△ABC三个顶点坐标分别为A（-1，3），B（-1，1），C（-3，2），以原点O为位似中心，将△ABC放大为原来的2倍得到△A1B1C1，请在第四象限内画出△A1B1C1，并写出A1、B1、C1三点的坐标．
如图，在四边形纸片ABCD中．∠A=130°，∠B=60°，现将其右下角向内折出△FGE，折痕为EF，恰使GF∥AD，GE∥CD，则∠C为
如图，一艘轮船在A处看见巡逻艇M在其北偏东58°的方向上，此时一艘客船在B处看见巡逻艇M在其北偏东12°的方向上，则此时从巡逻艇上看这两艘船的视角∠AMB=
如图，Rt△ADB中，∠D=90°，∠A=32°，C为边AD上一点，C与点A、D不重合，设∠ACB的度数为x，则x的取值范围是