题目内容
5.已知一次函数y=kx+b的图象经过点A(1,3),在y轴上的截距是5(1)求y与x轴的函数关系式;
(2)设一次函数y=kx+b的图象与x轴交于B点,求△OAB的面积.
分析 (1)根据题意列出关于k、b的二元一次方程组,通过解该方程组来求k、b的值;
(2)利用三角形的面积公式求得△OAB的面积即可.
解答 解:(1)由题意得$\left\{\begin{array}{l}{k+b=3}\\{b=5}\end{array}\right.$或$\left\{\begin{array}{l}{k+b=3}\\{b=-5}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=-2}\\{b=5}\end{array}\right.$或$\left\{\begin{array}{l}{k=8}\\{b=-5}\end{array}\right.$,
∴y与x轴的函数关系式为y=-2x+5或y=8x-5.
(2)当y=0时,
-2x+5=0,x=$\frac{5}{2}$;
8x-5=0,x=$\frac{5}{8}$;
∴△OAB的面积为$\frac{15}{4}$或$\frac{15}{16}$.
点评 本题考查了待定系数法求一次函数的解析式,一次函数图象上点的坐标特征.待定系数法求函数的解析式:先根据条件列出关于字母系数的方程,解方程求解即可得到函数解析式.

练习册系列答案
相关题目
13.已知圆O的直径是方程x2-5x-24=0的根,且点A到圆心O的距离为6,则点A在( )
| A. | 圆O上 | B. | 圆O内 | C. | 圆O外 | D. | 无法确定 |
15.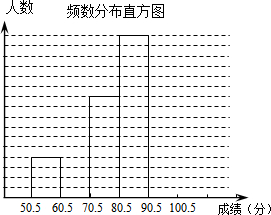 为了让学生了解党的十八大精神,某中学举行了一次“社会主义核心价值观暨八礼四仪知识竞赛”,共有1000名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成的频数分布表和频数分布直方图,解答下列问题:
为了让学生了解党的十八大精神,某中学举行了一次“社会主义核心价值观暨八礼四仪知识竞赛”,共有1000名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成的频数分布表和频数分布直方图,解答下列问题:
(1)a=10,b=0.24;
(2)补全频数分布直方图;
(3)在该问题中的样本容量是多少?答:50.
(4)若成绩在90分以上(不含90分)为优秀,则该校成绩优秀的约为240人?
 为了让学生了解党的十八大精神,某中学举行了一次“社会主义核心价值观暨八礼四仪知识竞赛”,共有1000名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成的频数分布表和频数分布直方图,解答下列问题:
为了让学生了解党的十八大精神,某中学举行了一次“社会主义核心价值观暨八礼四仪知识竞赛”,共有1000名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成的频数分布表和频数分布直方图,解答下列问题:| 频数分布表 | ||
| 分组 | 频数 | 频率 |
| 50.5~60.5 | 4 | 0.08 |
| 60.5~70.5 | 8 | 0.16 |
| 70.5~80.5 | a | 0.20 |
| 80.5~90.5 | 16 | 0.32 |
| 90.5~100.5 | 12 | b |
(2)补全频数分布直方图;
(3)在该问题中的样本容量是多少?答:50.
(4)若成绩在90分以上(不含90分)为优秀,则该校成绩优秀的约为240人?
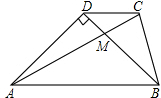 如图所示,在梯形ABCD中,AB∥CD,两对角线交于M,若AD=BD,AC=AB,∠ADB=90°,试说明:
如图所示,在梯形ABCD中,AB∥CD,两对角线交于M,若AD=BD,AC=AB,∠ADB=90°,试说明: 如图,OC⊥OD,∠2=54°08′,则∠1=35°52′.
如图,OC⊥OD,∠2=54°08′,则∠1=35°52′. 如图,在⊙O中,弦AB垂直平分半径OC,垂足为D,OC=2,则AB的长为2$\sqrt{3}$.
如图,在⊙O中,弦AB垂直平分半径OC,垂足为D,OC=2,则AB的长为2$\sqrt{3}$.