题目内容
6．已知△ABC中，∠C=90°，AC=6，BC=8，则AB边上的高等于4.8．分析 根据勾股定理求出AB的长，再根据面积法求出CD的长．
解答 
解：如图，
∵AC=6，BC=8，
∴AB=$\sqrt{{6}^{2}+{8}^{2}}$=10，
∴$\frac{1}{2}$AC•BC=$\frac{1}{2}$AB•CD，
∴6×8=10CD，
∴CD=$\frac{48}{10}$=4.8．
故答案为4.8．
点评 本题考查了勾股定理、三角形的面积，熟悉面积法是解题的关键．
练习册系列答案
相关题目
16．
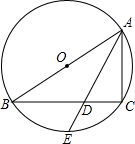如图，AB是⊙O的直径，点C在⊙O上，∠BAC的平分线交⊙O于E，交BC于D．若⊙O的半径为5，AC=6，那么DE的长为（ ）
如图，AB是⊙O的直径，点C在⊙O上，∠BAC的平分线交⊙O于E，交BC于D．若⊙O的半径为5，AC=6，那么DE的长为（ ）| A． | $\frac{9}{5}$$\sqrt{5}$ | B． | $\sqrt{5}$ | C． | 2 | D． | $\sqrt{3}$ |
如图，AB∥DE，若∠B=130°，∠D=30°，则∠BCF=100°．
1．下列命题是真命题的个数有（ ）
①直角三角形的两锐角互余；
②如果两个三角形的对应角相等，那么这两个三角形全等；
③在直角三角形中，若两条直角边长为n2-1和2n，则斜边长为n2+1；
④等腰三角形面积为12，底边上的高为4，则腰长为5．
①直角三角形的两锐角互余；
②如果两个三角形的对应角相等，那么这两个三角形全等；
③在直角三角形中，若两条直角边长为n2-1和2n，则斜边长为n2+1；
④等腰三角形面积为12，底边上的高为4，则腰长为5．
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
11．下列命题中，逆命题是真命题的是（ ）
| A． | 两直线平行，内错角相等 | |
| B． | 如果两个角都是直角，那么他们相等 | |
| C． | 全等三角形对应角都相等 | |
| D． | 如果x=1，那么|x|=1 |
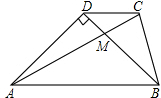如图所示，在梯形ABCD中，AB∥CD，两对角线交于M，若AD=BD，AC=AB，∠ADB=90°，试说明：