题目内容
16. 如图,在平面直角坐标系中,△ABC的三个顶点坐标都在格点上,且$△{A_1}{B_1}C_1^{\;}$与△ABC关于原点O成中心对称.
如图,在平面直角坐标系中,△ABC的三个顶点坐标都在格点上,且$△{A_1}{B_1}C_1^{\;}$与△ABC关于原点O成中心对称.(1)请直接写出A1的坐标(3,-4);并画出$△{A_1}{B_1}C_1^{\;}$.
(2)P(a,b)是△ABC的AC边上一点,将△ABC平移后点P的对称点P'(a+2,b-6),请画出平移后的△A2B2C2.
(3)若$△{A_1}{B_1}C_1^{\;}$和△A2B2C2关于某一点成中心对称,则对称中心的坐标为(1,-3).
分析 (1)直接利用关于原点对称点的性质得出对应点位置进而得出答案;
(2)直接利用平移规律得出△ABC平移后的位置;
(3)利用所画三角形连接对应点得出对称中心.
解答  解:(1)如图所示:△A1B1C1即为所求,A1(3,-4);
解:(1)如图所示:△A1B1C1即为所求,A1(3,-4);
故答案为:(3,-4);
(2)如图所示:△A2B2C2即为所求;
(3)如图所示:中心对称点O′的坐标为:(1,-3).
故答案为:(1,-3).
点评 此题主要考查了平移变换以及旋转变换,正确得出对应点位置是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
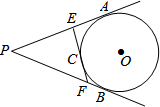 如图,PA、PB分别与⊙O相切于点A、B,⊙O的切线EF分别交PA、PB于点E、F,切点为C,若PA=5cm,则△PEF的周长为10cm.
如图,PA、PB分别与⊙O相切于点A、B,⊙O的切线EF分别交PA、PB于点E、F,切点为C,若PA=5cm,则△PEF的周长为10cm. 如图,已知直线L1∥L2,直线L3和直线L1、L2交于点C和D,在C、D之间有一点P.
如图,已知直线L1∥L2,直线L3和直线L1、L2交于点C和D,在C、D之间有一点P. 图中的两个三角形全等吗?为什么?
图中的两个三角形全等吗?为什么?