题目内容
4.如图,数轴上有A、B、C、D四点,其中与实数$\sqrt{10}-5$最接近的数所对应的点是( )
| A. | A | B. | B | C. | C | D. | D |
分析 先求出$\sqrt{10}$--5的取值范围,进而可得出结论.
解答 解:∵9<10<16,
∴3<$\sqrt{10}$<4,
∴-2<$\sqrt{10}$-5<-1,
∴点B与实数$\sqrt{10}-5$最接近.
故选B.
点评 本题考查的是实数与数轴,熟知实数与数轴上的点是一一对应关系是解答此题的关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
12.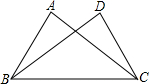 如图,△ABC≌△DCB,点A与点D,点B与点C对应,如果AC=6cm,AB=3cm,那么DC的长为( )
如图,△ABC≌△DCB,点A与点D,点B与点C对应,如果AC=6cm,AB=3cm,那么DC的长为( )
 如图,△ABC≌△DCB,点A与点D,点B与点C对应,如果AC=6cm,AB=3cm,那么DC的长为( )
如图,△ABC≌△DCB,点A与点D,点B与点C对应,如果AC=6cm,AB=3cm,那么DC的长为( )| A. | 3cm | B. | 5cm | C. | 6cm | D. | 无法确定 |
19.下列计算正确的是( )
| A. | 6x2•3xy=9x3y | B. | (2ab2)•(-3ab)=-a2b3 | C. | (mn)2•(-m2n)=-m3n3 | D. | (-3x2y)(-3xy)=9x3y2 |
9.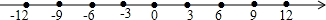 我们知道:|a|表示数轴上,数a的点到原点的距离.爱动脑筋的小明联系绝对值的概念和“|a|=|a-0|”,进而提出这样的问题:数轴上,数a的点到数1点的距离,是不是可以表示为|a-1|?小明的想法是否正确呢?让我们一起来探究吧!
我们知道:|a|表示数轴上,数a的点到原点的距离.爱动脑筋的小明联系绝对值的概念和“|a|=|a-0|”,进而提出这样的问题:数轴上,数a的点到数1点的距离,是不是可以表示为|a-1|?小明的想法是否正确呢?让我们一起来探究吧!
步骤一:实验与操作:
(1)已知点A、B在数轴上分别表示a、b.填写表格
步骤二:观察与猜想:
(2)观察上表:猜想A、B两点之间的距离可以表示为|a-b|(用a、b的代数式表示)
步骤三:理解与应用:
(3)动点A从原点出发向数轴负方向运动,同时,动点B也从原点出发向数轴正方向运动.运动到3秒时,两点相距15个单位长度.已知动点A、B的速度之比是3:2(速度单位:1个单位长度/秒).
①求两个动点运动的速度;
②A、B两动点运动到3秒时停止运动,请在数轴上标出此时A、B两点的位置;
③若A、B两动点分别从(2)中标出的位置再次同时开始在数轴上运动,运动速度不变,运动方向不限.问:经过几秒后,A、B两动点之间相距4个单位长度.
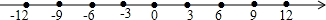 我们知道:|a|表示数轴上,数a的点到原点的距离.爱动脑筋的小明联系绝对值的概念和“|a|=|a-0|”,进而提出这样的问题:数轴上,数a的点到数1点的距离,是不是可以表示为|a-1|?小明的想法是否正确呢?让我们一起来探究吧!
我们知道:|a|表示数轴上,数a的点到原点的距离.爱动脑筋的小明联系绝对值的概念和“|a|=|a-0|”,进而提出这样的问题:数轴上,数a的点到数1点的距离,是不是可以表示为|a-1|?小明的想法是否正确呢?让我们一起来探究吧!步骤一:实验与操作:
(1)已知点A、B在数轴上分别表示a、b.填写表格
| a | 3 | -5 | 5 | -10 | -5.5 | … |
| b | 7 | 0 | -1 | 2 | -1.5 | … |
| A、B两点之间的距离 | 4 | 5 | … |
(2)观察上表:猜想A、B两点之间的距离可以表示为|a-b|(用a、b的代数式表示)
步骤三:理解与应用:
(3)动点A从原点出发向数轴负方向运动,同时,动点B也从原点出发向数轴正方向运动.运动到3秒时,两点相距15个单位长度.已知动点A、B的速度之比是3:2(速度单位:1个单位长度/秒).
①求两个动点运动的速度;
②A、B两动点运动到3秒时停止运动,请在数轴上标出此时A、B两点的位置;
③若A、B两动点分别从(2)中标出的位置再次同时开始在数轴上运动,运动速度不变,运动方向不限.问:经过几秒后,A、B两动点之间相距4个单位长度.
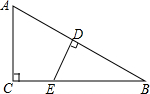 在Rt△ABC中,∠C=90°,点E在BC上,ED⊥AB于点D,求证:$\frac{AC}{AB}$=$\frac{DE}{BE}$.
在Rt△ABC中,∠C=90°,点E在BC上,ED⊥AB于点D,求证:$\frac{AC}{AB}$=$\frac{DE}{BE}$. 如图,△ABC中,AB=AC,D,E分别是AC、AB上的点,且BD=BC,AD=DE=EB,求∠A的度数.
如图,△ABC中,AB=AC,D,E分别是AC、AB上的点,且BD=BC,AD=DE=EB,求∠A的度数.