题目内容
12.若点P1(x1,y1),P2(x2,y2)在反比例函数y=$\frac{k}{x}$(k>0)的图象上,且x1=-x2,则( )| A. | y1<y2 | B. | y1=y2 | C. | y1>y2 | D. | y1=-y2 |
分析 根据反比例函数图象上点的坐标特征得到y1=$\frac{k}{{x}_{1}}$,y2=$\frac{k}{{x}_{2}}$,根据x1=-x2解得y1=$\frac{k}{{x}_{1}}$=-$\frac{k}{{x}_{2}}$,从而求得y1=-y2.
解答 解:∵点P1(x1,y1),P2(x2,y2)在反比例函数y=$\frac{k}{x}$(k>0)的图象上,
∴y1=$\frac{k}{{x}_{1}}$,y2=$\frac{k}{{x}_{2}}$,
∵x1=-x2,
∴y1=$\frac{k}{{x}_{1}}$=-$\frac{k}{{x}_{2}}$
∴y1=-y2.
故选D.
点评 本题考查了反比例函数图象上点的坐标特征:反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
2.将下列多项式因式分解,结果中不含因式x-1的是( )
| A. | x2-1 | B. | x(x-2)+(2-x) | C. | x2-2 | D. | x2-2x+1 |
7. 如图,△ABC中,AB=5,BC=3,AC=4,以点C为圆心的圆与AB相切,则⊙C的半径为( )
如图,△ABC中,AB=5,BC=3,AC=4,以点C为圆心的圆与AB相切,则⊙C的半径为( )
 如图,△ABC中,AB=5,BC=3,AC=4,以点C为圆心的圆与AB相切,则⊙C的半径为( )
如图,△ABC中,AB=5,BC=3,AC=4,以点C为圆心的圆与AB相切,则⊙C的半径为( )| A. | 2.3 | B. | 2.4 | C. | 2.5 | D. | 2.6 |
17. 某几何体的三视图如图所示,这个几何体是( )
某几何体的三视图如图所示,这个几何体是( )
 某几何体的三视图如图所示,这个几何体是( )
某几何体的三视图如图所示,这个几何体是( )| A. | 圆锥 | B. | 圆柱 | C. | 三棱柱 | D. | 三棱锥 |
1.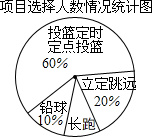 某班同学响应“阳光体育运动”号召,利用课外活动积极参加体育锻炼,每位同学从长跑、铅球、立定跳远、篮球定时定点投篮中任选一项进行了训练,训练前后都进行了测试,现将项目选择情况及训练后篮球定时定点投篮进球数进行整理,作出如下统计图表.
某班同学响应“阳光体育运动”号召,利用课外活动积极参加体育锻炼,每位同学从长跑、铅球、立定跳远、篮球定时定点投篮中任选一项进行了训练,训练前后都进行了测试,现将项目选择情况及训练后篮球定时定点投篮进球数进行整理,作出如下统计图表.
训练后篮球定点投篮测试进球统计表
请你根据图表中的信息回答下列问题:
(1)训练后篮球定时定点投篮人均进球数为5个;
(2)选择长跑训练的人数占全班人数的百分比是10%,该班共有同学40人;
(3)根据测试资料,参加篮球定时定点投篮的学生训练后比训练前的人均进球增加了25%,求参加训练之前的人均进球数.
 某班同学响应“阳光体育运动”号召,利用课外活动积极参加体育锻炼,每位同学从长跑、铅球、立定跳远、篮球定时定点投篮中任选一项进行了训练,训练前后都进行了测试,现将项目选择情况及训练后篮球定时定点投篮进球数进行整理,作出如下统计图表.
某班同学响应“阳光体育运动”号召,利用课外活动积极参加体育锻炼,每位同学从长跑、铅球、立定跳远、篮球定时定点投篮中任选一项进行了训练,训练前后都进行了测试,现将项目选择情况及训练后篮球定时定点投篮进球数进行整理,作出如下统计图表.训练后篮球定点投篮测试进球统计表
| 进球数(个) | 8 | 7 | 6 | 5 | 4 | 3 |
| 人数 | 2 | 1 | 4 | 7 | 8 | 2 |
(1)训练后篮球定时定点投篮人均进球数为5个;
(2)选择长跑训练的人数占全班人数的百分比是10%,该班共有同学40人;
(3)根据测试资料,参加篮球定时定点投篮的学生训练后比训练前的人均进球增加了25%,求参加训练之前的人均进球数.
2.某中学九年级舞蹈兴趣小组8名学生的身高分别为(单位:cm):168,165,168,166,170,170,176,170,则下列说法错误的是( )
| A. | 这组数据的众数是170 | |
| B. | 这组数据的中位数是169 | |
| C. | 这组数据的平均数是169 | |
| D. | 若从8名学生中任选1名学生参加校文艺会演,则这名学生的身高不低于170的概率为$\frac{1}{2}$ |
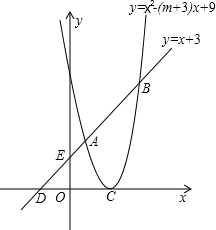 如图,已知抛物线y=x2-(m+3)x+9的顶点C在x轴正半轴上,一次函数y=x+3与抛物线交于A、B两点,与x、y轴交于D、E两点.
如图,已知抛物线y=x2-(m+3)x+9的顶点C在x轴正半轴上,一次函数y=x+3与抛物线交于A、B两点,与x、y轴交于D、E两点.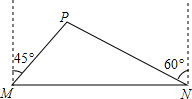 我市准备在相距2千米的M,N两工厂间修一条笔直的公路,但在M地北偏东45°方向、N地北偏西60°方向的P处,有一个半径为0.6千米的住宅小区(如图),问修筑公路时,这个小区是否有居民需要搬迁?(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
我市准备在相距2千米的M,N两工厂间修一条笔直的公路,但在M地北偏东45°方向、N地北偏西60°方向的P处,有一个半径为0.6千米的住宅小区(如图),问修筑公路时,这个小区是否有居民需要搬迁?(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)